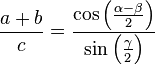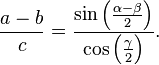Mollweide's formula

Figure 1 – A triangle. The angles α, β, and γ are respectively opposite the sides a, b, and c.

In trigonometry, Mollweide's formula, sometimes referred to in older texts as Mollweide's equations,[1] named after Karl Mollweide, is a set of two relationships between sides and angles in a triangle.[2] It can be used to check solutions of triangles.[3]

Let a, b, and c be the lengths of the three sides of a triangle. Let α, β, and γ be the measures of the angles opposite those three sides respectively. Mollweide's formula states that

\frac{a + b}{c} = \frac{\cos\left(\frac{\alpha - \beta}{2}\right)}{\sin\left(\frac{\gamma}{2}\right)}

and

\frac{a - b}{c} = \frac{\sin\left(\frac{\alpha - \beta}{2}\right)}{\cos\left(\frac{\gamma}{2}\right)}.

Each of these identities uses all six parts of the triangle—the three angles and the lengths of the three sides.

See also

References

  1. ↑ Ernest Julius Wilczynski, Plane Trigonometry and Applications, Allyn and Bacon, 1914, page 102
  2. ↑ Michael Sullivan, Trigonometry, Dellen Publishing Company, 1988, page 243.
  3. ↑ Ernest Julius Wilczynski, Plane Trigonometry and Applications, Allyn and Bacon, 1914, page 105

Additional reading

This article is issued from Wikipedia - version of the Wednesday, December 02, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.