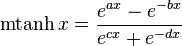Modified hyperbolic tangent

The modified hyperbolic tangent (mtanh or mth) is a special S-shaped function based on the hyperbolic tangent, given by

\operatorname{mtanh}x = \frac {e^{ax} - e^{-bx}} {e^{cx} + e^{-dx}}

This function was proposed by Elena Soboleva (of Ukraine) as a utility function for multi-objective optimization and choice modelling in decision-making.[1][2][3]

In other papers it is used for approximation of current-voltage characteristics of field-effect transistors[4] and light-emitting diodes.

With parameters a = b = c = d = 1 the modified hyperbolic tangent function reduces to the conventional tanh(x) function, whereas for a = b = 1 and c = d = 0, the term becomes equal to sinh(x).

See also

Wikimedia Commons has media related to Hyperbolic functions.

References

  1. ↑ Soboleva, Elena. V.; Beskorovainyi, V. V. (2008). The utility function in problems of structural optimization of distributed objects (in Russian). Kharkiv University of Air Force. p. 121.
  2. ↑ Soboleva, Elena V. (2009). The S-shaped utility function of individual criteria for multi-objective decision-making in design (in Russian). Kharkiv National University of Radioelectronics. p. 247.
  3. ↑ Beskorovainyi, V. V.; Soboleva, Elena V. (2010). ИДЕНТИФИКАЦИЯ ЧАСТНОй ПОлЕЗНОСТИ МНОГОФАКТОРНЫХ АлЬТЕРНАТИВ С ПОМОЩЬЮ S-ОБРАЗНЫХ ФУНКЦИй [Identification of utility functions in multi-objective choice modelling by using S-shaped functions] (PDF) (in Russian). Kharkiv National University of Radioelectronics. pp. 50–54. УДК 519.688: 004.896; БИОНИКА ИНТЕЛЛЕКТА 2010. No 1 (72).
  4. ↑ Tuev, Vasily I.; Uzhanin, Maxim V. (2009). ПРИМЕНЕНИЕ МОДИФИЦИРОВАННОЙ ФУНКЦИИ ГИПЕРБОЛИЧЕСКОГО ТАНГЕНСА ДЛЯ АППРОКСИМАЦИИ ВОЛЬТАМПЕРНЫХ ХАРАКТЕРИСТИК ПОЛЕВЫХ ТРАНЗИСТОРОВ [Using modified hyperbolic tangent function to approximate the current-voltage characteristics of field-effect transistors] (in Russian). Tomsk Politehnic University. pp. 135–138. 4/314/2009. Retrieved 2015-11-05.
This article is issued from Wikipedia - version of the Saturday, November 07, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.