Minimum rank of a graph

In mathematics, the minimum rank is a graph parameter 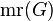$\operatorname{mr}(G)$ for any graph G. It was motivated by the Colin de Verdière's invariant.

Definition

The adjacency matrix of a given undirected graph is a symmetric matrix whose rows and columns both correspond to the vertices of the graph. Its coefficients are all 0 or 1, and the coefficient in row i and column j is nonzero whenever vertex i is adjacent to vertex j in the graph. More generally, one can define a generalized adjacency matrix to be any matrix of real numbers with the same pattern of nonzeros. 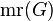The minimum rank of the graph $G$ is denoted by $\operatorname{mr} (G)$ and is defined as the smallest rank of any generalized adjacency matrix of the graph.

Properties

The minimum rank of a graph is always at most equal to n − 1, where n is the number of vertices in the graph.^[1]
For every induced subgraph H of a given graph G, the minimum rank of H is at most equal to the minimum rank of G.^[2]
If a given graph is not connected, then its minimum rank is the sum of the minimum ranks of its connected components.^[3]
The minimum rank is a graph invariant: any two isomorphic graphs necessarily have the same minimum rank.

Characterization of known graph families

Several families of graphs may be characterized in terms of their minimum ranks.

For $n\geq 2$ , the complete graph K_n on n vertices has minimum rank one. The only graphs that are connected and have minimum rank one are the complete graphs.^[4]
A path graph P_n on n vertices has minimum rank n − 1. The only n-vertex graphs with minimum rank n − 1 are the path graphs.^[5]
A cycle graph C_n on n vertices has minimum rank n − 2.^[6]
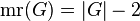Let $G$ be a 2-connected graph. Then $\operatorname{mr}(G)=|G|-2$ if and only if $G$ is a linear 2-tree.^[7]
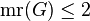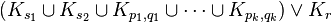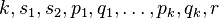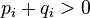A graph $G$ has $\operatorname{mr}(G)\leq 2$ if and only if the complement of $G$ is of the form $(K_{s_1}\cup K_{s_2}\cup K_{p_1,q_1}\cup \cdots \cup K_{p_k,q_k} ) \vee K_r$ for appropriate nonnegative integers $k, s_1, s_2, p_1, q_1,\ldots , p_k, q_k, r$ with $p_i+q_i>0$ for all $i=1,\ldots, k$ .^[8]

Notes

↑ Fallat-Hogben, Observation 1.2.
↑ Fallat-Hogben, Observation 1.6.
↑ Fallat-Hogben, Observation 1.6.
↑ Fallat-Hogben, Observation 1.2.
↑ Fallat-Hogben, Corollary 1.5.
↑ Fallat-Hogben, Observation 1.6.
↑ Fallat-Hogben, Theorem 2.10.
↑ Fallat-Hogben, Theorem 2.9.

References

Fallat, Shaun; Hogben, Leslie, "The minimum rank of symmetric matrices described by a graph: A survey", Linear Algebra and its Applications 426 (2007) (PDF), pp. 558–582 .

This article is issued from Wikipedia - version of the Sunday, January 31, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.