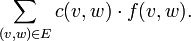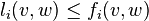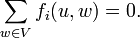Circulation problem
The circulation problem and its variants are a generalisation of network flow problems, with the added constraint of a lower bound on edge flows, and with flow conservation also being required for the source and sink (i.e. there are no special nodes). In variants of the problem, you have multiple commodities flowing through the network, and a cost on the flow.
Definition
Given flow network 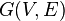 with:
with:
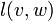 , lower bound on flow from node
, lower bound on flow from node 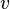 to node
to node  ,
,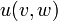 , upper bound on flow from node
, upper bound on flow from node 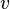 to node
to node  ,
, , cost of a unit of flow on
, cost of a unit of flow on 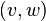
and the constraints:
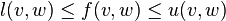 ,
,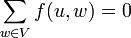 (flow cannot appear or disappear in nodes).
(flow cannot appear or disappear in nodes).
Finding a flow assignment satisfying the constraints gives a solution to the given circulation problem.
In the minimum cost variant of the problem, minimize
Multi-commodity circulation
In a multi-commodity circulation problem, you also need to keep track of the flow of the individual commodities:
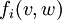
The flow of commodity  from
from 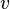 to
to  .
.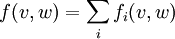
The total flow.
There is also a lower bound on each flow of commodity.
The conservation constraint must be upheld individually for the commodities:
Solution
For the circulation problem, many polynomial algorithms have been developed (e.g., Edmonds and Karp, 1972; Tarjan 1987-1988). Tardos found the first strongly polynomial algorithm.[1]
For the case of multiple commodities, the problem is NP-complete for integer flows.[2] For fractional flows, it is solvable in polynomial time, as one can formulate the problem as a linear program.
Related problems
Below are given some problems, and how to solve them with the general circulation setup given above.
- Minimum cost multi-commodity circulation problem - Using all constraints given above.
- Minimum cost circulation problem - Use a single commodity
- Multi-commodity circulation - Solve without optimising cost.
- Simple circulation - Just use one commodity, and no cost.
- Multi-commodity flow - If
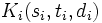 denotes a demand of
denotes a demand of  for commodity
for commodity  from
from 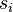 to
to  , create an edge
, create an edge 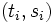 with
with  for all commodities
for all commodities  . Let
. Let  for all other edges.
for all other edges. - Minimum cost multi-commodity flow problem - As above, but minimize the cost.
- Minimum cost flow problem - As above, with 1 commodity.
- Maximum flow problem - Set all costs to 0, and add an edge from the sink
 to the source
to the source  with
with 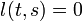 ,
,  ∞ and
∞ and 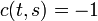 .
. - Minimum cost maximum flow problem - First find the maximum flow amount
 . Then solve with
. Then solve with  and
and 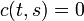 .
. - Single-source shortest path - Let
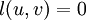 and
and  for all edges in the graph, and add an edge
for all edges in the graph, and add an edge 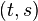 with
with 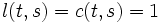 and
and 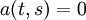 .
. - All-pairs shortest path - Let all capacities be unlimited, and find a flow of 1 for
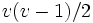 commodities, one for each pair of nodes.
commodities, one for each pair of nodes.
References
- ↑ Éva Tardos. "A strongly polynomial minimum cost circulation algorithm". Combinatorica 5: 247–255. doi:10.1007/BF02579369.
- ↑ S. Even and A. Itai and A. Shamir (1976). "On the complexity of time table and multi-commodity flow problems". SIAM Journal on Computing (SIAM) 5 (4): 691–703. doi:10.1137/0205048.