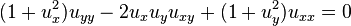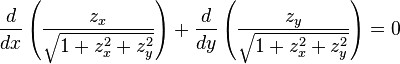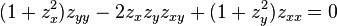Minimal surface
In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to (see definitions below) having a mean curvature of zero.
The term "minimal surface" is used because these surfaces originally arose as surfaces that minimized total surface area subject to some constraint. Physical models of area-minimizing minimal surfaces can be made by dipping a wire frame into a soap solution, forming a soap film, which is a minimal surface whose boundary is the wire frame. However the term is used for more general surfaces that may self-intersect or do not have constraints. For a given constraint there may also exist several minimal surfaces with different areas (for example, see minimal surface of revolution): the standard definitions only relate to a local optimum, not a global optimum.
Definitions

Minimal surfaces can be defined in several equivalent ways in R3. The fact that they are equivalent serves to demonstrate how minimal surface theory lies at the crossroads of several mathematical disciplines, especially differential geometry, calculus of variations, potential theory, complex analysis and mathematical physics.[1]
- Local least area definition: A surface M ⊂ R3 is minimal if and only if every point p ∈ M has a neighbourhood with least-area relative to its boundary.
Note that this property is local: there might exist other surfaces that minimize area better with the same global boundary.
- Variational definition: A surface M ⊂ R3 is minimal if and only if it is a critical point of the area functional for all compactly supported variations.
This definition makes minimal surfaces a 2-dimensional analogue to geodesics.
- Soap film definition: A surface M ⊂ R3 is minimal if and only if every point p ∈ M has a neighbourhood Dp which is equal to the unique idealized soap film with boundary ∂Dp
By the Young–Laplace equation the curvature of a soap film is proportional to the difference in pressure between the sides: if it is zero, the membrane has zero mean curvature. Note that spherical bubbles are not minimal surfaces as per this definition: while they minimize total area subject to a constraint on internal volume, they have a positive pressure.

- Mean curvature definition: A surface M ⊂ R3 is minimal if and only if its mean curvature vanishes identically.
A direct implication of this definition is that every point on the surface is a saddle point with equal and opposite principal curvatures.
- Differential equation definition: A surface M ⊂ R3 is minimal if and only if it can be locally expressed as the graph of a solution of
The partial differential equation in this definition was originally found in 1762 by Lagrange,[2] and Jean Baptiste Meusnier discovered in 1776 that it implied a vanishing mean curvature.[3]
- Energy definition: A conformal immersion X: M → R3 is minimal if and only if it is a critical point of the Dirichlet energy for all compactly supported variations, or equivalently if any point p ∈ M has a neighbourhood with least energy relative to its boundary.
This definition ties minimal surfaces to harmonic functions and potential theory.
- Harmonic definition: If X = (x1, x2, x3): M → R3 is an isometric immersion of a Riemann surface into 3-space, then X is said to be minimal whenever xi is a harmonic function on M for each i.
A direct implication of this definition and the maximum principle for harmonic functions is that there are no compact complete minimal surfaces in R3.
- Gauss map definition: A surface M ⊂ R3 is minimal if and only if its stereographically projected Gauss map g: M → C ∪ {∞} is meromorphic with respect to the underlying Riemann surface structure, and M is not a piece of a sphere.
This definition uses that the mean curvature is half of the trace of the shape operator, which is linked to the derivatives of the Gauss map. If the projected Gauss map obeys the Cauchy–Riemann equations then either the trace vanishes or every point of M is umbilic, in which case it is a piece of a sphere.
- Mean curvature flow definition: Minimal surfaces are the critical points for the mean curvature flow.[4]
The local least area and variational definitions allow extending minimal surfaces to other Riemannian manifolds than R3.
History
Minimal surface theory originates with Lagrange who in 1762 considered the variational problem of finding the surface z = z(x, y) of least area stretched across a given closed contour. He derived the Euler–Lagrange equation for the solution
He did not succeed in finding any solution beyond the plane. In 1776 Jean Baptiste Marie Meusnier discovered that the helicoid and catenoid satisfy the equation, and that the differential expression corresponds to twice the mean curvature of the surface, concluding that surfaces with zero mean curvature are area-minimizing.
By expanding Lagrange's equation to
Gaspard Monge and Legendre in 1795 derived representation formulas for the solution surfaces. While these were successfully used by Heinrich Scherk in 1830 to derive his surfaces, they were generally regarded as practically unusable. Catalan proved in 1842/43 that the helicoid is the only ruled minimal surface.
Progress had been fairly slow until the middle of the century, when the Björling problem was solved using complex methods. The "first golden age" of minimal surfaces began. Schwarz found the solution of the Plateau problem for a regular quadrilateral in 1865 and for a general quadrilateral in 1867 (allowing the construction of his periodic surface families) using complex methods. Weierstrass and Enneper developed more useful representation formulas, firmly linking minimal surfaces to complex analysis and harmonic functions. Other important contributions came from Beltrami, Bonnet, Darboux, Lie, Riemann, Serret and Weingarten.
Between 1925 and 1950 minimal surface theory revived, now mainly aimed at nonparametric minimal surfaces. The complete solution of the Plateau problem by Jesse Douglas and Tibor Radó was a major milestone. Bernstein's problem and Robert Osserman's work on complete minimal surfaces of finite total curvature were also important.
Another revival began in the 1980s. One cause was the discovery in 1982 by Celso Costa of a surface that disproved the conjecture that the plane, the catenoid, and the helicoid are the only complete embedded minimal surfaces in R3 of finite topological type. This not only stimulated new work on using the old parametric methods, but also demonstrated the importance of computer graphics to visualise the studied surfaces and numerical methods to solve the "period problem" (when using the conjugate surface method to determine surface patches that can be assembled into a larger symmetric surface, certain parameters need to be numerically matched to produce an embedded surface). Another cause was the verification by H. Karcher that the triply periodic minimal surfaces originally described empirically by Alan Schoen in 1970 actually exist. This has led to a rich menagerie of surface families and methods of deriving new surfaces from old, for example by adding handles or distorting them.
Currently the theory of minimal surfaces has diversified to minimal submanifolds in other ambient geometries, becoming relevant to mathematical physics (e.g. the positive mass conjecture, the Penrose conjecture) and three-manifold geometry (e.g. the Smith conjecture, the Poincaré conjecture, the Thurston Geometrization Conjecture).
Examples
Classical examples of minimal surfaces include:
- the plane, which is a trivial case
- catenoids: minimal surfaces made by rotating a catenary once around its directrix
- helicoids: A surface swept out by a line rotating with uniform velocity around an axis perpendicular to the line and simultaneously moving along the axis with uniform velocity
Surfaces from the 19th century golden age include:
- Schwarz minimal surfaces: triply periodic surfaces that fill R3
- Riemann's minimal surface: A posthumously described periodic surface
- the Enneper surface
- the Henneberg surface: the first non-orientable minimal surface
- Bour's minimal surface
Modern surfaces include:
- the Gyroid: One of Schoen's 1970 surfaces, a triply periodic surface of particular interest for liquid crystal structure
- the Saddle tower family: generalisations of Scherk's second surface
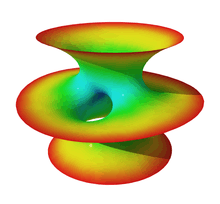
- Costa's minimal surface: Famous conjecture disproof. Described 1982 by Celso Costa and later visualized by Jim Hoffman. Jim Hoffman, David Hoffman and William Meeks III then extended the definition to produce a family of surfaces with different rotational symmetries.
- the Chen–Gackstatter surface family, adding handles to the Enneper surface.
Generalisations and links to other fields
Minimal surfaces can be defined in other manifolds than R3, such as hyperbolic space, higher-dimensional spaces or Riemannian manifolds.
The definition of minimal surfaces can be generalized/extended to cover constant-mean-curvature surfaces: surfaces with a constant mean curvature, which need not equal zero.
In discrete differential geometry discrete minimal surfaces are studied: simplicial complexes of triangles that minimize their area under small perturbations of their vertex positions.[5] Such discretizations are often used to approximate minimal surfaces numerically, even if no closed form expressions are known.
Brownian motion on a minimal surface leads to probabilistic proofs of several theorems on minimal surfaces.[6]
Minimal surfaces have become an area of intense scientific study, especially in the areas of molecular engineering and materials science, due to their anticipated applications in self-assembly of complex materials.
Minimal surfaces play a role in general relativity. The apparent horizon (marginally outer trapped surface) is a minimal hypersurface, linking the theory of black holes to minimal surfaces and the Plateau problem.[7][8]
Minimal surfaces are part of the generative design toolbox used by modern designers. In architecture there has been much interest in tensile structures, which are closely related to minimal surfaces. A famous example is the Olympiapark in Münich by Frei Otto, inspired by soap surfaces.
In the art world, minimal surfaces have been extensively explored in the sculpture of Robert Engman (1927– ), Robert Longhurst (1949– ), and Charles O. Perry (1929–2011), among others.
See also
- Bernstein's problem
- Bilinear interpolation
- Bryant surface
- Curvature
- Enneper–Weierstrass parameterization
- Harmonic map
- Harmonic morphism
- Plateau's problem
- Schwarz minimal surface
- Soap bubble
- Surface Evolver
- Stretched grid method
- Tensile structure
- Triply periodic minimal surface
- Weaire–Phelan structure
References
- ↑ Meeks, William H., III; Pérez, Joaquín (2011). "The classical theory of minimal surfaces". Bull. Amer. Math. Soc. 48 (3): 325–407. doi:10.1090/s0273-0979-2011-01334-9. MR 2801776.
- ↑ J. L. Lagrange. Essai d'une nouvelle methode pour determiner les maxima et les minima des formules integrales indefinies. Miscellanea Taurinensia 2, 325(1):173{199, 1760.
- ↑ J. B. Meusnier. Mémoire sur la courbure des surfaces. Mém. Mathém. Phys. Acad. Sci. Paris, prés. par div. Savans, 10:477-510, 1785. Presented in 1776.
- ↑ Colding, Tobias H.; Minicozzi, William P., II (2004). "The Space of Embedded Minimal Surfaces of Fixed Genus in a 3-manifold. II. Multi-valued Graphs in Disks". Ann. of Math. 160 (1): 69–92. doi:10.4007/annals.2004.160.69. MR 2119718.
- ↑ Pinkall, Ulrich; Polthier, Konrad (1993). "Computing Discrete Minimal Surfaces and Their Conjugates". Experimental Mathematics 2 (1): 15–36. MR 1246481.
- ↑ Neel, Robert (2009). "A martingale approach to minimal surfaces". Journal of Functional Analysis 256 (8): 2440–2472. arXiv:0805.0556. doi:10.1016/j.jfa.2008.06.033. MR 2502522.
- ↑ Chruściel, Piotr T.; Galloway, Gregory J.; Pollack, Daniel (2010). "Mathematical general relativity: a sampler". Bull. Amer. Math. Soc. 47: 567–638. arXiv:1004.1016. doi:10.1090/S0273-0979-2010-01304-5. MR 2721040.
- ↑ Eichmair, Michael (2009). "The Plateau problem for marginally outer trapped surfaces". Journal of Differential Geometry 83 (3): 551–584. arXiv:0711.4139. MR 2581357.
Further reading
- Osserman, Robert (1986). A Survey of Minimal Surfaces (Second ed.). New York: Dover Publications, Inc. ISBN 0-486-64998-9. MR 0852409. (Introductory text for surfaces in n-dimensions, including n=3; requires strong calculus abilities but no knowledge of differential geometry.)
- Karcher, Hermann; Polthier, Konrad (1995). "Touching Soap Films - An introduction to minimal surfaces". Retrieved December 27, 2006. (graphical introduction to minimal surfaces and soap films.)
- Various (2000-). "EG-Models". Retrieved September 28, 2004. Check date values in:
|date=(help) (Online journal with several published models of minimal surfaces) - Stewart Dickson (1996). "Scientific Concretization; Relevance to the Visually Impaired Student". VR in the School, Volume 1, Number 4. Retrieved April 15, 2006. (Describes the discovery of Costa's surface)
- Martin Steffens and Christian Teitzel. "Grape Minimal Surface Library". Retrieved October 27, 2008. (A collection of minimal surfaces)
- David Hoffman, Jim Hoffman; et al. "Scientific Graphics Project". Retrieved April 24, 2006. (An collection of minimal surfaces with classical and modern examples)
- Jacek Klinowski. "Periodic Minimal Surfaces Gallery". Retrieved February 2, 2009. (An collection of minimal surfaces with classical and modern examples)
- Dierkes, Ulrich; Hildebrandt, Stefan; Sauvigny, Friedrich (2010). Minimal Surfaces. Grundlehren der Mathematischen Wissenschaften 339. With assistance and contributions by A. Küster and R. Jakob (Second ed.). Heidelberg: Springer. doi:10.1007/978-3-642-11698-8. ISBN 978-3-642-11697-1. MR 2566897. (Review of minimal surface theory, in particularly boundary value problems. Contains extensive references to the literature.)
External links
- Hazewinkel, Michiel, ed. (2001), "Minimal surface", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- 3D-XplorMath-J Homepage — Java program and applets for interactive mathematical visualisation
- Gallery of rotatable minimal surfaces
- WebGL-based Gallery of rotatable/zoomable minimal surfaces
| ||||||||