Minimal prime ideal
In mathematics, especially in the area of algebra known as commutative algebra, certain prime ideals called minimal prime ideals play an important role in understanding rings and modules. The notion of height and Krull's principal ideal theorem use minimal primes.
Definition
A prime ideal P is said to be a minimal prime ideal over an ideal I if it is minimal among all prime ideals containing I. (Note that we do not exclude I even if it is a prime ideal.) A prime ideal is said to be a minimal prime ideal if it is a minimal prime ideal over the zero ideal.
A minimal prime ideal over an ideal I in a Noetherian ring R is precisely a minimal associated prime (also called isolated prime) of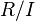 
; this follows for instance from the primary decomposition of I.
Examples
- In a commutative artinian ring, every maximal ideal is a minimal prime ideal.
- In an integral domain, the only minimal prime ideal is the zero ideal.
- In the ring Z of integers, the minimal prime ideals over a nonzero principal ideal (n) are the principal ideals (p), where p is a prime divisor of n. The only minimal prime ideal over the zero ideal is the zero ideal itself. Similar statements hold for any principal ideal domain.
- If I is a p-primary ideal (for example, a power of p), then p is the unique minimal prime ideal over I.
Properties
All rings are assumed to be commutative and unital.
- Every proper ideal I in a ring has at least one minimal prime ideal above it. The proof of this fact uses Zorn's lemma (Kaplansky 1974, p. 6). Any maximal ideal containing I is prime, and such ideals exist, so the set of prime ideals containing I is non-empty. The intersection of a decreasing chain of prime ideals is prime. Therefore, the set of prime ideals containing I has a minimal element, which is a minimal prime over I.
- Emmy Noether showed that in a Noetherian ring, there are only finitely many minimal prime ideals over any given ideal. (Kaplansky 1974, p. 59), (Eisenbud 1995, p. 47) The fact remains true if "Noetherian" is replaced by the ascending chain conditions on radical ideals.
- The radical
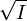of any proper ideal I coincides with the intersection of the minimal prime ideals over I. (Kaplansky 1974, p. 16). - The set of zero divisors of a given ring contains the union of the minimal prime ideals (Kaplansky 1974, p. 57).
- Krull's principal ideal theorem describes important properties of minimal prime ideals.
References
- Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94268-1, MR 1322960
- Kaplansky, Irving (1974), Commutative rings, University of Chicago Press, MR 0345945