Mingarelli identity

In the field of ordinary differential equations, the Mingarelli identity (coined by Philip Hartman^[1]) is a theorem that provides criteria for the oscillation and non-oscillation of solutions of some linear differential equations in the real domain. It extends the Picone identity from two to three or more differential equations of the second order. Its most basic form appears here.

The identity

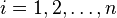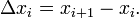Consider the $n$ solutions of the following (uncoupled) system of second order linear differential equations over the t-interval [a, b]. $(p_{i}(t)x_{i}^{\prime })^{\prime }+q_{i}(t)x_{i}=0,\,\,\,\,\,\,\,\,\,\,x_{i}(a)=1,\,\,x_{i}^{\prime }(a)=R_{i}\,$ where $i=1,2,\ldots ,n$ . Let $\Delta$ denote the forward difference operator, i.e., $\Delta x_{i}=x_{i+1}-x_{i}.$ The second order difference operator is found by iterating the first order operator as in 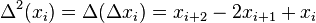$\Delta ^{2}(x_{i})=\Delta (\Delta x_{i})=x_{i+2}-2x_{i+1}+x_{i}$ , with a similar definition for the higher iterates.

Leaving out the independent variable t for convenience, and assuming the 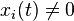$x_{i}(t)\neq 0$ on (a, b], there holds the identity,^[2]

{\begin{aligned}x_{n-1}^{2}\Delta ^{n-1}(p_{1}r_{1})]_{a}^{b}&=\int _{a}^{b}(x_{n-1}^{\prime })^{2}\Delta ^{n-1}(p_{1})-\int _{a}^{b}x_{n-1}^{2}\Delta ^{n-1}(q_{1})-\sum _{k=0}^{n-1}C(n-1,k)(-1)^{n-k-1}\int _{a}^{b}p_{k+1}W^{2}(x_{k+1},x_{n-1})/x_{k+1}^{2},\end{aligned}}

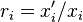where $r_{i}=x_{i}^{\prime }/x_{i}$ is a logarithmic derivative, 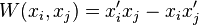$W(x_{i},x_{j})=x_{i}^{\prime }x_{j}-x_{i}x_{j}^{\prime }$ , is a Wronskian and the 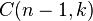$C(n-1,k)$ are binomial coefficients. When 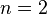$n=2$ this reduces to the Picone identity.

The above identity leads quickly to the following comparison theorem for three linear differential equations,^[2] extending the Sturm–Picone comparison theorem.

Let 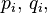$p_{i},\,q_{i},\,$ i = 1, 2, 3 be real-valued continuous functions on the interval [a, b] and let

$(p_{1}(t)x_{1}^{\prime })^{\prime }+q_{1}(t)x_{1}=0,\,\,\,\,\,\,\,\,\,\,x_{1}(a)=1,\,\,x_{1}^{\prime }(a)=R_{1}\,$
$(p_{2}(t)x_{2}^{\prime })^{\prime }+q_{2}(t)x_{2}=0,\,\,\,\,\,\,\,\,\,\,x_{2}(a)=1,\,\,x_{2}^{\prime }(a)=R_{2}\,$
$(p_{3}(t)x_{3}^{\prime })^{\prime }+q_{3}(t)x_{3}=0,\,\,\,\,\,\,\,\,\,\,x_{3}(a)=1,\,\,x_{3}^{\prime }(a)=R_{3}\,$

be three homogeneous linear second order differential equations in self-adjoint form with

p_{i}(t)>0\,

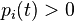for each i and for all t in [a, b], and where the

R_{i}

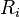are arbitrary real numbers.

Assume that for all t in [a, b] we have,

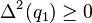\Delta ^{2}(q_{1})\geq 0

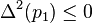\Delta ^{2}(p_{1})\leq 0

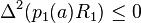\Delta ^{2}(p_{1}(a)R_{1})\leq 0

If 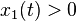$x_{1}(t)>0$ on [a, b], and 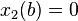$x_{2}(b)=0$ , then any solution 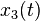$x_{3}(t)$ has at least one zero in [a, b].

References

↑ Clark D.N., G. Pecelli, and R. Sacksteder 1981
1 2 Mingarelli 1979, p. 223

Clark D.N., G. Pecelli, and R. Sacksteder (1981). Contributions to Analysis and Geometry. Baltimore, USA: Johns Hopkins University Press.

Mingarelli, Angelo B. (1979). "Some extensions of the Sturm–Picone theorem". Comptes Rendus Math. Rep. Acad. Sci. Canada (Toronto, Ontario, Canada: The Royal Society of Canada) 1 (4): 223–226.

This article is issued from Wikipedia - version of the Sunday, July 19, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.