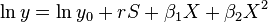Mincer earnings function
The Mincer earnings function is a single-equation model that explains earnings as a function of schooling and experience, named after Jacob Mincer.[1][2] The equation has been examined on many datasets and Thomas Lemieux argues it is "one of the most widely used models in empirical economics". Typically the logarithm of earnings is modelled as the sum of years of education and a quadratic function of "years of potential experience".[3][4]
Where the variables have the following meanings; 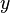 is earnings (
is earnings ( is the earnings of someone with no education and no experience);
is the earnings of someone with no education and no experience); 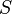 is years of schooling;
is years of schooling;  is years of potential labour market experience.[3]
is years of potential labour market experience.[3]
Sherwin Rosen, in his article celebrating Mincer's contribution, memorably noted that when data was interrogated using this equation one might describe them as having been Mincered.[5]
References
- ↑ Mincer, Jacob (1958). "Investment in Human Capital and Personal Income Distribution". Journal of Political Economy 66 (4): 281–302. doi:10.1086/258055. JSTOR 1827422.
- ↑ Mincer, J. (1974). Schooling, Experience and Earnings. New York: National Bureau of Economic Research.
- 1 2 Lemieux, Thomas. (2006) "The 'Mincer equation' Thirty Years after Schooling, Experience, and Earnings" in Jacob Mincer: A Pioneer of Modern Labor Economics, Shoshanna Grossbard, ed., Springer: New York. pp. 127–145.
- ↑ Heckman, James J.; Lochner, Lance J.; Todd, Petra E. (2003). "Fifty Years of Mincer Earnings Regressions". NBER Working Paper No. 9732. doi:10.3386/w9732.
- ↑ Rosen, Sherwin (1992). "Distinguished Fellow: Mincering Labor Economics". Journal of Economic Perspectives 6 (2): 157–170. doi:10.1257/jep.6.2.157. JSTOR 2138414.
Further reading
- Borjas, George J. (2000). Labor Economics (Second ed.). New York: McGraw-Hill. pp. 264–266. ISBN 0-07-231198-3.
- Heckman, J.; Lochner, L.; Todd, P. (2006). "Earnings Functions, Rates of Return and Treatment Effects: The Mincer Equation and Beyond". Handbook of the Economics of Education 1. Amsterdam: North-Holland. pp. 307–458. ISBN 0-08-046566-8.
- Polachek, Solomon W. (2007). "Earnings Over the Lifecycle: The Mincer Earnings Function and Its Applications" (PDF). IZA Discussion Paper No. 3181.