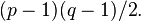Milnor conjecture (topology)

For Milnor's conjecture about K-theory, see Milnor conjecture.

In knot theory, the Milnor conjecture says that the slice genus of the 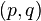(p, q) torus knot is

(p-1)(q-1)/2.

It is in a similar vein to the Thom conjecture.

It was first proved by gauge theoretic methods by Peter Kronheimer and Tomasz Mrowka.[1] Jacob Rasmussen later gave a purely combinatorial proof using Khovanov homology, by means of the s-invariant.[2]

References

  1. ↑ Kronheimer, P. B.; Mrowka, T. S. (1993), "Gauge theory for embedded surfaces, I", Topology 32 (4): 773–826, doi:10.1016/0040-9383(93)90051-V.
  2. ↑ Rasmussen, Jacob A. (2004). "Khovanov homology and the slice genus". arXiv:math.GT/0402131..


This article is issued from Wikipedia - version of the Saturday, March 16, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.