Miller cylindrical projection

A Miller projection of the Earth.
The Miller cylindrical projection is a modified Mercator projection, proposed by Osborn Maitland Miller (1897–1979) in 1942. The latitude is scaled by a factor of 4⁄5, projected according to Mercator, and then the result is multiplied by 5⁄4 to retain scale along the equator.[1] Hence:
or inversely,
where λ is the longitude from the central meridian of the projection, and φ is the latitude.[2] Meridians are thus about 0.733 the length of the equator.
In GIS applications, this projection is known as: "EPSG:54003 - World Miller Cylindrical"
See also
References
- ↑ Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, 1993, pp. 179, 183, ISBN 0-226-76747-7.
- ↑ "Miller Cylindrical Projection". Wolfram MathWorld. Retrieved 25 March 2015.
External links
- Table of examples and properties of all common projections, from radicalcartography.net
- An interactive Java Applet to study the metric deformations of the Miller Projection.
- Math formulae information
- Spatial information
- Historical information
This article is issued from Wikipedia - version of the Thursday, January 07, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
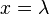
![y = \frac{5}{4}\ln\left[\tan\left(\frac{\pi}{4} + \frac{2\varphi}{5}\right)\right] = \frac{5}{4}\sinh^{-1}\left(\tan\frac{4\varphi}{5}\right)](../I/m/658bf3239c8d360a19fd81b833c28b55.png)

