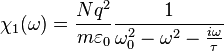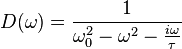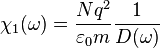Miller's Rule (optics)

In optics, Miller's Rule is an empirical rule which gives an estimate of the order of magnitude of the nonlinear coefﬁcient.

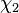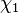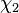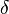More formally, it states that the coefficient of the second order electric susceptibility response ( $\chi_{\text{2}}$ ) is proportional to the product of the first-order susceptibilities ( $\chi_{\text{1}}$ ) at the three frequencies which $\chi_{\text{2}}$ is dependent upon.^[1] The proportionality coefficient is known as Miller's coefficient $\delta$ .

Definition

The first order susceptibility response is given by:

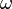\chi_{\text{1}}(\omega)=\frac{Nq^2}{m\varepsilon_0} \frac{1}{\omega_\mathrm{0}^2-\omega^2-\tfrac{i\omega}{\tau}}

where:

$\omega$ is the frequency of oscillation of the electric field;
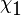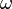$\chi_{\textrm{1}}$ is the first order electric susceptibility, as a function of $\omega$ ;
N is the number density of oscillating charge carriers (electrons);
q is the fundamental charge;
m is the mass of the oscillating charges, the electron mass;
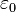$\varepsilon_0$ is the electric permittivity of free space;
i is the imaginary unit;
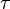$\tau$ is the free carrier relaxation time;

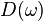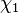For simplicity, we can define $D(\omega)$ , and hence rewrite $\chi_{\text{1}}$ :

D(\omega)=\frac{1}{\omega_\mathrm{0}^2-\omega^2-\tfrac{i\omega}{\tau}}

\chi_{\text{1}}(\omega)=\frac{Nq^2}{\varepsilon_0 m} \frac{1}{D(\omega)}

The second order susceptibility response is given by:

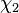\chi_{\text{2}}(2\omega)=\frac{Nq^3\zeta_2}{\varepsilon_0m^2} \frac{1}{D(2\omega)D(\omega)^2}

where $\zeta_2$ is the first anharmonicity coefficient. It is easy to show that we can thus express $\chi_{\text{2}}$ in terms of a product of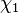 $\chi_{\text{1}}$

\chi_{\text{2}}(2\omega)=\frac{\varepsilon_0^2 m \zeta_2}{N^2q^3} \chi_{\text{1}}(\omega)\chi_{\text{1}}(\omega)\chi_{\text{1}}(2\omega)

The constant of proportionality between 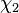$\chi_{\text{2}}$ and the product of 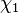$\chi_{\text{1}}$ at three different frequencies is Miller's coefficient:

\delta=\frac{\varepsilon_0^2 m \zeta_2}{N^2q^3}

References

↑ Boyd, Robert (2008). Nonlinear Optics. Academic Press. ISBN 0123694701.

This article is issued from Wikipedia - version of the Friday, June 20, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.