Metrical task system

Task systems are mathematical objects used to model the set of possible configuration of online algorithms. They were introduced by Borodin, Linial and Saks (1992) to model a variety of online problems. A task system determines a set of states and costs to change states. Task systems obtain as input a sequence of requests such that each request assigns processing times to the states. The objective of an online algorithm for task systems is to create a schedule that minimizes the overall cost incurred due to processing the tasks with respect to the states and due to the cost to change states.

If the cost function to change states is a metric, the task system is a metrical task system (MTS). This is the most common type of task systems. Metrical task systems generalize online problems such as paging, list accessing, and the k-server problem (in finite spaces).

Formal Definition

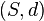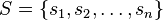A task system is a pair (S,d) where S=\{s_1,s_2,\dotsc,s_n\} is a set of states and 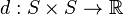d:S \times S \rightarrow \mathbb{R} is a distance function. If 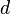d is a metric, 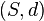(S,d) is a metrical task system. An input to the task system is a sequence 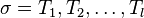\sigma = T_1,T_2,\dotsc,T_l such that for each 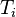i, T_i is a vector of n non-negative entries that determine the processing costs for the n states when processing the ith task.

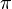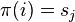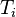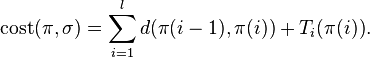
An algorithm for the task system produces a schedule \pi that determines the sequence of states. For instance, \pi(i)=s_j means that the ith task T_i is run in state s_j. The processing cost of a schedule is \mathrm{cost}(\pi,\sigma) = \sum_{i=1}^l d(\pi(i-1),\pi(i)) + T_i(\pi(i)).

The objective of the algorithm is to find a schedule such that the cost is minimized.

Known Results

As usual for online problems, the most common measure to analyze algorithms for metrical task systems is the competitive analysis, where the performance of an online algorithm is compared to the performance of an optimal offline algorithm. For deterministic online algorithms, there is a tight bound 2n-1 on the competitive ratio due to Borodin et al. (1992).

For randomized online algorithms, the competitive ratio is lower bounded by 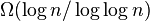\Omega(\log n / \log\log n) and upper bounded by 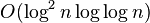O(\log^2 n \log\log n). The lower bound is due to Bartal et al. (2006,2005). The upper bound is due to Fiat and Mendel (2003) who improved upon a result of Bartal et al. (1997).

There are many results for various types of restricted metrics.

See also

References

This article is issued from Wikipedia - version of the Friday, August 07, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.