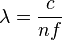Metre

This article is about the unit of length. For other uses of "metre" or "meter", see meter (disambiguation).
Metre
Unit system SI base unit
Unit of Length
Symbol m 
Unit conversions
1 m in ...... is equal to ...
   nm    1 0003 (1 000 000 000 nm)
   μm    1 0002 (1 000 000 μm)
   mm    1 0001 (1 000 mm)
   km    1 000−1 (0.001 km)
   Mm    1 000−2 (0.000 001 Mm)
   in    ≈ 39.3701
Look up metre in Wiktionary, the free dictionary.

The metre, or meter (American spelling), (from the Greek noun μέτρον, "measure") is the base unit of length in the International System of Units (SI). The SI unit symbol is m.[1] The metre is defined as the distance travelled by light in a specific fraction (1/299 792 458) of a second.[2]

The metre was originally defined in 1793 as one ten-millionth of the distance from the equator to the North Pole. In 1889, it was redefined in terms of a prototype metre bar (the actual bar used was subsequently changed twice). In 1960, the metre was redefined in terms of a certain number of wavelengths of a certain emission line of krypton-86. In 1983, the current definition was adopted.

The imperial inch is defined as 0.0254 metres (2.54 centimetres or 25.4 millimetres). One metre is about 3 3⁄8 inches longer than a yard, i.e. about 39 3⁄8 inches.

Spelling

Metre is the standard spelling of the metric unit for length in all English-speaking nations except the USA, which uses meter.[3]

Measuring devices (such as ammeter, speedometer) are spelled "-meter" in all countries.[4] The word "meter", signifying any such device, has the same derivation as the word "metre", denoting the unit of length.[5]

Etymology

The etymological roots of metre can be traced to the Greek verb μετρέω (metreo) (to measure, count or compare) and noun μέτρον (metron) (a measure), which were used for physical measurement, for poetic metre and by extension for moderation or avoiding extremism (as in "be measured in your response"). This range of uses is also found in Latin (metior, mensura), French (mètre, mesure), English and other languages. The motto ΜΕΤΡΩ ΧΡΩ (metro chro) in the seal of the International Bureau of Weights and Measures (BIMP), which was a saying of the Greek statesman and philosopher Pittacus of Mytilene and may be translated as "Use measure!", thus calls for both measurement and moderation.

History of definition

Main article: History of the metre

In 1668 the English cleric and philosopher John Wilkins proposed in an essay a decimal-based unit of length, the universal measure or standard based on a pendulum with a one-second period.[6] In 1670 Gabriel Mouton, Bishop of Lyon, also suggested a universal length standard with decimal multiples and divisions, to be based on a one-minute angle of the Earth's meridian arc or (as the Earth's circumference was not easy to measure) on a pendulum with a one-second period. In 1675, the Italian scientist Tito Livio Burattini, in his work Misura Universale, used the phrase metro cattolico ("universal measure"), derived from the Greek μέτρον καθολικόν (métron katholikón), to denote the standard unit of length derived from a pendulum.[7] As a result of the French Revolution, the French Academy of Sciences charged a commission with determining a single scale for all measures. On 7 October 1790 that commission advised the adoption of a decimal system, and on 19 March 1791 advised the adoption of the term mètre ("measure"), a basic unit of length, which they defined as equal to one ten-millionth of the distance between the North Pole and the Equator,[8][9][10][11] In 1793, the French National Convention adopted the proposal; this use of metre in English began at least as early as 1797.[12]

Belfry, Dunkirk—the northern end of the meridian arc
Fortress of Montjuïc—the southerly end of the meridian arc
Creating the metre-alloy in 1874 at the Conservatoire des Arts et Métiers. Present Henri Tresca, George Matthey, Saint-Claire Deville and Debray

Pendular

In 1668, Wilkins proposed using Christopher Wren's suggestion of defining the metre using a pendulum with a length which produced a half-period of one second, known as a 'seconds pendulum'. Christiaan Huygens had observed that length to be 38 Rijnland inches or 39.26 English inches. This is the equivalent of what is now known to be 997 mm.[6] No official action was taken regarding this suggestion.

Meridional

In the 18th century, there were two approaches to the definition of the standard unit of length. One favoured Wilkins approach: to define the metre in terms of the length of a pendulum which produced a half-period of one second. The other approach was to define the metre as one ten-millionth (1/10 000 000) of the length of a quadrant along the Earth's meridian; that is, the distance from the Equator to the North Pole. This means that the quadrant (a section/distance 1⁄4 of the Earth's circumference) would have been defined as exactly 10 000 000 metres (10 000 km) at that time, with the total circumference of the Earth defined as 40 000 000 metres (40 000 km). In 1791, the French Academy of Sciences selected the meridional definition over the pendular definition because the force of gravity varies slightly over the surface of the Earth, which affects the period of a pendulum.

To establish a universally accepted foundation for the definition of the metre, more accurate measurements of this meridian were needed. The French Academy of Sciences commissioned an expedition led by Jean Baptiste Joseph Delambre and Pierre Méchain, lasting from 1792 to 1799, which attempted to accurately measure the distance between a belfry in Dunkerque and Montjuïc castle in Barcelona to estimate the length of the meridian arc through Dunkerque. This portion of the meridian, assumed to be the same length as the Paris meridian, was to serve as the basis for the length of the half meridian connecting the North Pole with the Equator. The problem with this approach is that the exact shape of the Earth is not a simple mathematical shape, such as a sphere or oblate spheroid, at the level of precision required for defining a standard of length. The irregular and particular shape of the Earth smoothed to sea level is called a geoid, which literally means "Earth-shaped", but does not correspond to the actual shape of the earth, but rather is a mathematical model of its shape. Despite these issues, in 1793 France adopted this definition of the metre as its official unit of length based on provisional results from this expedition.

Prototype metre bar

In the 1870s and in light of modern precision, a series of international conferences was held to devise new metric standards. The Metre Convention (Convention du Mètre) of 1875 mandated the establishment of a permanent International Bureau of Weights and Measures (BIPM: Bureau International des Poids et Mesures) to be located in Sèvres, France. This new organisation was to construct and preserve a prototype metre bar, distribute national metric prototypes, and maintain comparisons between them and non-metric measurement standards. The organisation created such a bar in 1889 at the first General Conference on Weights and Measures (CGPM: Conférence Générale des Poids et Mesures), establishing the International Prototype Metre as the distance between two lines on a standard bar composed of an alloy of 90% platinum and 10% iridium, measured at the melting point of ice.[13]

However, it was later determined that the first prototype metre bar was short by about 200 micrometres because of miscalculation of the flattening of the Earth, making the prototype about 0.02% shorter than the original proposed definition of the metre. Regardless, this length became the standard. The original international prototype of the metre is still kept at the BIPM under the conditions specified in 1889.

Number of wavelengths of red-orange emission line of krypton-86

In 1893, the standard metre was first measured with an interferometer by Albert A. Michelson, the inventor of the device and an advocate of using some particular wavelength of light as a standard of length. By 1925, interferometry was in regular use at the BIPM. However, the International Prototype Metre remained the standard until 1960, when the eleventh CGPM defined the metre in the new International System of Units (SI) as equal to 1 650 763.73 wavelengths of the orange-red emission line in the electromagnetic spectrum of the krypton-86 atom in a vacuum.[14]

Distance travelled by light in a specified time

To further reduce uncertainty, the 17th CGPM in 1983 replaced the definition of the metre with its current definition, thus fixing the length of the metre in terms of the second and the speed of light:

The metre is the length of the path travelled by light in vacuum during a time interval of 1/299792458 of a second.[2]

This definition fixed the speed of light in vacuum at exactly 299792458 metres per second (≈300 000 km/s). An intended by-product of the 17th CGPM's definition was that it enabled scientists to compare lasers accurately using frequency, resulting in wavelengths with one-fifth the uncertainty involved in the direct comparison of wavelengths, because interferometer errors were eliminated. To further facilitate reproducibility from lab to lab, the 17th CGPM also made the iodine-stabilised helium–neon laser "a recommended radiation" for realising the metre.[15] For the purpose of delineating the metre, the BIPM currently considers the HeNe laser wavelength, λHeNe, to be 632.99121258 nm with an estimated relative standard uncertainty (U) of 2.1×10−11.[15][16][17] This uncertainty is currently one limiting factor in laboratory realisations of the metre, and it is several orders of magnitude poorer than that of the second, based upon the caesium fountain atomic clock (U = 5×10−16).[18] Consequently, a realisation of the metre is usually delineated (not defined) today in labs as 1579800.762042(33) wavelengths of helium-neon laser light in a vacuum, the error stated being only that of frequency determination.[15] This bracket notation expressing the error is explained in the article on measurement uncertainty.

Practical realisation of the metre is subject to uncertainties in characterising the medium, to various uncertainties of interferometry, and to uncertainties in measuring the frequency of the source.[19] A commonly used medium is air, and the National Institute of Standards and Technology (NIST) has set up an online calculator to convert wavelengths in vacuum to wavelengths in air.[20] As described by NIST, in air, the uncertainties in characterising the medium are dominated by errors in measuring temperature and pressure. Errors in the theoretical formulas used are secondary.[21] By implementing a refractive index correction such as this, an approximate realisation of the metre can be implemented in air, for example, using the formulation of the metre as 1579800.762042(33) wavelengths of helium-neon laser light in vacuum, and converting the wavelengths in a vacuum to wavelengths in air. Of course, air is only one possible medium to use in a realisation of the metre, and any partial vacuum can be used, or some inert atmosphere like helium gas, provided the appropriate corrections for refractive index are implemented.[22]

The metre is defined as the path length travelled by light in a given time and practical laboratory length measurements in metres are determined by counting the number of wavelengths of laser light of one of the standard types that fit into the length,[23] and converting the selected unit of wavelength to metres. Three major factors limit the accuracy attainable with laser interferometers for a length measurement:[19][26]

Of these, the last is peculiar to the interferometer itself. The conversion of a length in wavelengths to a length in metres is based upon the relation:

\lambda = \frac{c}{n f} \

which converts the unit of wavelength λ to metres using c, the speed of light in a vacuum in m/s. Here n is the refractive index of the medium in which the measurement is made; and f is the measured frequency of the source. Although conversion from wavelengths to metres introduces an additional error in the overall length due to measurement error in determining the refractive index and the frequency, the measurement of frequency is one of the most accurate measurements available.[26]

Timeline

Closeup of National Prototype Metre Bar No. 27, made in 1889 by the International Bureau of Weights and Measures (BIPM) and given to the United States, which served as the standard for defining all units of length in the US from 1893 to 1960
Definitions of the metre since 1795[30]
Basis of definition Date Absolute
uncertainty		 Relative
uncertainty
1/10 000 000 part of the quadrant along the meridian, measurement by Delambre and Méchain (443.296 lines) 1795 500–100 μm 10−4
First prototype Mètre des Archives platinum bar standard 1799 50–10 μm 10−5
Platinum-iridium bar at melting point of ice (1st CGPM) 1889 0.2–0.1 µm (200-100 nm) 10−7
Platinum-iridium bar at melting point of ice, atmospheric pressure, supported by two rollers (7th CGPM) 1927 n.a. n.a.
Hyperfine atomic transition; 1650763.73 wavelengths of light from a specified transition in krypton-86 (11th CGPM) 1960 4 nm 4x10−9[31]
Length of the path travelled by light in a vacuum in 1/299 792 458 of a second (17th CGPM) 1983 0.1 nm 10−10

SI prefixed forms of metre

SI prefixes are often employed to denote decimal multiples and submultiples of the metre, as shown in the table below. As indicated in the table, some are commonly used, while others are not. Long distances are usually expressed in km, astronomical units (149.6 Gm), light-years (10 Pm), or parsecs (31 Pm), rather than in Mm, Gm, Tm, Pm, Em, Zm or Ym; "30 cm", "30 m", and "300 m" are more common than "3 dm", "3 dam", and "3 hm", respectively.

The terms micron and (occasionally) millimicron are often used instead of micrometre (μm) and nanometre (nm), but this practice is officially discouraged.[32]

SI multiples for metre (m)
Submultiples Multiples
Value SI symbol Name Value SI symbol Name
10−1 m dm decimetre 101 m dam decametre
10−2 m cm centimetre 102 m hm hectometre
10−3 m mm millimetre 103 m km kilometre
10−6 m µm micrometre 106 m Mm megametre
10−9 m nm nanometre 109 m Gm gigametre
10−12 m pm picometre 1012 m Tm terametre
10−15 m fm femtometre 1015 m Pm petametre
10−18 m am attometre 1018 m Em exametre
10−21 m zm zeptometre 1021 m Zm zettametre
10−24 m ym yoctometre 1024 m Ym yottametre
Common prefixed units are in bold face.

Equivalents in other units

Metric unit
expressed in non-SI units		 Non-SI unit
expressed in metric units
1 metre ≈ 1.0936 yard 1 yard≡ 0.9144 metre
1 metre ≈ 39.370 inches 1 inch≡ 0.0254 metre
1 centimetre ≈ 0.39370 inch 1 inch≡ 2.54 centimetres
1 millimetre ≈ 0.039370 inch 1 inch≡ 25.4 millimetres
1 metre ≡ 1×1010ångström 1 ångström≡ 1×10−10 metre
1 nanometre ≡ 10ångström 1 ångström≡ 100 picometres

Within this table, "inch" and "yard" mean "international inch" and "international yard",[33] respectively, though approximate conversions in the left-hand column hold for both international and survey units.

"≈" means "is approximately equal to";
"≡" means "equal by definition" or "is exactly equal to."

One metre is exactly equivalent to 10 000/254 inches and to 10 000/9 144 yards.

A simple mnemonic aid exists to assist with conversion, as three "3"s:

1 metre is nearly equivalent to 3 feet 3 3⁄8 inches.[34] This gives an overestimate of 0.125 mm. However, the practice of memorising such conversion formulas has been discouraged in favour of practice and visualisation of metric units.

The ancient Egyptian cubit was about 0.5 m (surviving rods are 523–529 mm). Scottish and English definitions of the ell (two cubits) were 941 mm (0.941 m) and 1 143 mm (1.143 m), respectively. The ancient Parisian toise (fathom) was slightly shorter than 2 m, and was standardised at exactly 2 m in the mesures usuelles system, such that 1 m was exactly 1⁄2 toise. The Russian versta was 1.0668 km. The Swedish mil was 10.688 km, but was changed to 10 km when Sweden converted to metric units.

See also

Notes

  1. ↑ "Base unit definitions: Meter". National Institute of Standards and Technology. Retrieved 2010-09-28.
  2. 1 2 "17th General Conference on Weights and Measures (1983), Resolution 1.". Retrieved 2012-09-19.
  3. ↑ The most recent official brochure about the International System of Units (SI), written in French by the Bureau international des poids et mesures, International Bureau of Weights and Measures (BIPM) uses the spelling metre; an English translation, included to make the SI standard "more widely accessible" also uses the spelling metre.(BIPM, 2006, p. 130ff) However, in 2008 the U.S. English translation published by the U.S. National Institute of Standards and Technology (NIST) chose to use the spelling meter in accordance with the United States Government Printing Office Style Manual. The Metric Conversion Act of 1975 gives the Secretary of Commerce of the US the responsibility of interpreting or modifying the SI for use in the US. The Secretary of Commerce delegated this authority to the Director of the National Institute of Standards and Technology (Turner). In 2008, NIST published the US version (Taylor and Thompson, 2008a) of the English text of the eighth edition of the BIPM publication Le Système international d'unités (SI) (BIPM, 2006). In the NIST publication, the spellings "meter", "liter" and "deka" are used rather than "metre", "litre" and "deca" as in the original BIPM English text (Taylor and Thompson (2008a), p. iii). The Director of the NIST officially recognised this publication, together with Taylor and Thompson (2008b), as the "legal interpretation" of the SI for the United States (Turner). Thus, the spelling metre is referred to as the "international spelling"; the spelling meter, as the "American spelling".
  4. ↑ Cambridge Advanced Learner's Dictionary. Cambridge University Press. 2008. Retrieved 2012-09-19., s.v. ammeter, meter, parking meter, speedometer.
  5. ↑ American Heritage Dictionary of the English Language (3rd ed.). Boston: Houghton Mifflin. 1992., s.v. meter.
  6. 1 2 An Essay Towards a Real Character, and A Philosophical Language — John Wilkins F.R.S. 1668, pp191-192
  7. ↑ George Sarton (1935). "The First Explanation of Decimal Fractions and Measures (1585). Together with a History of the Decimal Idea and a Facsimile (No. XVII) of Stevin's Disme". Isis 23 (1): 153–244. doi:10.1086/346940.
  8. ↑ ('decimalization is not of the essence of the metric system; the real significance of this is that it was the first great attempt to define terrestrial units of measure in terms of an unvarying astronomical or geodetic constant.) The metre was in fact defined as one ten millionth of one quarter of the earth's circumference at sea-level.' Joseph Needham, Science and Civilisation in China, Cambridge University Press, 1962 vol.4, pt.1, p.42.
  9. ↑ Agnoli, Paolo (2004). Il senso della misura: la codifica della realtà tra filosofia, scienza ed esistenza umana (in Italian). Armando Editore. pp. 93–94,101. Retrieved 2015-10-13.
  10. ↑ "Rapport sur le choix d'une unité de mesure, lu à l'Académie des sciences, le 19 mars 1791" (in French). Gallica.bnf.fr. 2007-10-15. Retrieved 2013-03-25.
  11. ↑ Paolo Agnoli and Giulio D’Agostini,'Why does the meter beat the second?,' December, 2004 pp.1-29.
  12. ↑ Oxford English Dictionary, Clarendon Press 2nd ed.1989, vol.IX p.697 col.3.
  13. ↑ National Institute of Standards and Technology 2003; Historical context of the SI: Unit of length (meter)
  14. ↑ Marion, Jerry B. (1982). Physics For Science and Engineering. CBS College Publishing. p. 3. ISBN 4-8337-0098-0.
  15. 1 2 3 "Iodine (λ≈633 nm)" (PDF). MEP (Mise en Pratique). BIPM. 2003. Retrieved 16 December 2011.
  16. ↑ The term "relative standard uncertainty" is explained by NIST on their web site: "Standard Uncertainty and Relative Standard Uncertainty". The NIST Reference on constants, units, and uncertainties: Fundamental physical constants. NIST. Retrieved 19 December 2011.
  17. ↑ National Research Council 2010
  18. ↑ National Institute of Standards and Technology 2011.
  19. 1 2 A more detailed listing of errors can be found in Beers, John S; Penzes, William B (December 1992). "§4 Re-evaluation of measurement errors" (PDF). NIST length scale interferometer measurement assurance; NIST document NISTIR 4998. pp. 9 ff. Retrieved 17 December 2011.
  20. ↑ The formulas used in the calculator and the documentation behind them are found at "Engineering metrology toolbox: Refractive index of air calculator". NIST. September 23, 2010. Retrieved 16 December 2011. The choice is offered to use either the modified Edlén equation or the Ciddor equation. The documentation provides a discussion of how to choose between the two possibilities.
  21. ↑ "§VI: Uncertainty and range of validity". Engineering metrology toolbox: Refractive index of air calculator. NIST. September 23, 2010. Retrieved 16 December 2011.
  22. ↑ Dunning, F. B.; Hulet, Randall G. (1997). "Physical limits on accuracy and resolution: setting the scale". Atomic, molecular, and optical physics: electromagnetic radiation, Volume 29, Part 3. Academic Press. p. 316. ISBN 0-12-475977-7. The error [introduced by using air] can be reduced tenfold if the chamber is filled with an atmosphere of helium rather than air.
  23. ↑ The BIPM maintains a list of recommended radiations on their web site.[24][25]
  24. ↑ "Recommended values of standard frequencies". BIPM. 9 September 2010. Retrieved 22 January 2012.
  25. ↑ National Physical Laboratory 2010
  26. 1 2 Zagar, 1999, pp. 6–65ff
  27. ↑ Barbrow & Judson 1976, appendix 6.
  28. ↑ Taylor and Thompson (2008a), Appendix 1, p. 70.
  29. ↑ Taylor and Thompson (2008a), Appendix 1, p. 77.
  30. ↑ Cardarelli 2003
  31. ↑ Definition of the metre Resolution 1 of the 17th meeting of the CGPM (1983)
  32. ↑ Taylor & Thompson 2003, p. 11.
  33. ↑ Astin & Karo 1959.
  34. ↑ Well-known conversion, publicised at time of metrication.

References

Further reading

Wikimedia Commons has media related to Metre.
This article is issued from Wikipedia - version of the Saturday, February 06, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.