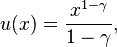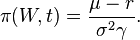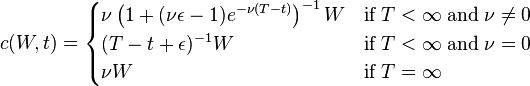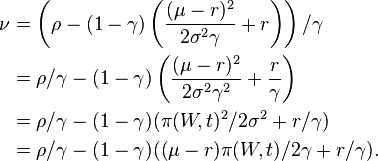Merton's portfolio problem
Merton's portfolio problem is a well known problem in continuous-time finance and in particular intertemporal portfolio choice. An investor must choose how much to consume and must allocate his wealth between stocks and a risk-free asset so as to maximize expected utility. The problem was formulated and solved by Robert C. Merton in 1969 both for finite lifetimes and for the infinite case.[1] Research has continued to extend and generalize the model to include factors like transaction costs and bankruptcy.
Problem statement
The investor lives from time 0 to time T; his wealth at time t is denoted Wt. He starts with a known initial wealth W0 (which may include the present value of wage income). At time t he must choose what amount of his wealth to consume, ct, and what fraction of wealth to invest in a stock portfolio, πt (the remaining fraction 1 − πt being invested in the risk-free asset).
The objective is
where E is the expectation operator, u is a known utility function (which applies both to consumption and to the terminal wealth, or bequest, WT) and ρ is the subjective discount rate.
The wealth evolves according to the stochastic differential equation
where r is the risk-free rate, (μ, σ) are the expected return and volatility of the stock market and dBt is the increment of the Wiener process, i.e. the stochastic term of the SDE.
The utility function is of the constant relative risk aversion (CRRA) form:
where 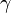 is a constant which expresses the investor's risk aversion: the higher the gamma, the more reluctance to own stocks.
is a constant which expresses the investor's risk aversion: the higher the gamma, the more reluctance to own stocks.
Consumption cannot be negative: ct ≥ 0, while πt is unrestricted (that is borrowing or shorting stocks is allowed).
Investment opportunities are assumed constant, that is r, μ, σ are known and constant, in this (1969) version of the model, although Merton allowed them to change in his intertemporal CAPM (1973).
Solution
Somewhat surprisingly for an optimal control problem, a closed-form solution exists. The optimal consumption and stock allocation depend on wealth and time as follows:
(Note that W and t do not appear on the right-hand side; this implies that a constant fraction of wealth is invested in stocks, no matter what the age or prosperity of the investor).
where  and
and
The variable  is the subjective utility discount rate.[2]:401)
is the subjective utility discount rate.[2]:401)
Extensions
Many variations of the problem have been explored, but most do not lead to a simple closed-form solution.
- Flexible retirement age can be taken into account.[3]
- A utility function other than CRRA can be used.
- Transaction costs can be introduced. For proportional transaction costs the problem was solved by Davis and Norman in 1990.[4] It is one of the few cases of stochastic singular control where the solution is known. For a graphical representation, the amount invested in each of the two assets can be plotted on the x- and y-axes; three diagonal lines through the origin can be drawn: the upper boundary, the Merton line and the lower boundary. The Merton line represents portfolios having the stock/bond proportion derived by Merton in the absence of transaction costs. As long as the point which represents the current portfolio is near the Merton line, i.e. between the upper and the lower boundary, no action needs to be taken. When the portfolio crosses above the upper or below the lower boundary, one should rebalance the portfolio to bring it back to that boundary. In 1994 Shreve and Soner provided an analysis of the problem via the Hamilton–Jacobi–Bellman equation and its viscosity solutions.[5]
- When there are fixed transaction costs the problem was addressed by Eastman and Hastings in 1988.[6] A numerical solution method was provided by Schroder in 1995.[7]
- Finally Morton and Pliska[8] considered trading costs that are proportional to the wealth of the investor for logarithmic utility. Although this cost structure seems unrepresentative of real life transaction costs, it can be used to find approximate solutions in cases with additional assets,[9] for example individual stocks, where it becomes difficult or intractable to give exact solutions for the problem.
- The assumption of constant investment opportunities can be relaxed. This requires a model for how
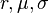 change over time. An interest rate model could be added and would lead to a portfolio containing bonds of different maturities. Some authors have added a stochastic volatility model of stock market returns.
change over time. An interest rate model could be added and would lead to a portfolio containing bonds of different maturities. Some authors have added a stochastic volatility model of stock market returns.
- Bankruptcy can be incorporated. This problem was solved by Karatzas, Lehoczky, Sethi and Shreve in 1986.[10] Many models incorporating bankruptcy are collected in Sethi (1997).[11]
References
- ↑ Merton, R. C. (1 August 1969). "Lifetime Portfolio Selection under Uncertainty: the Continuous-Time Case". The Review of Economics and Statistics 51 (3): 247–257. doi:10.2307/1926560. ISSN 0034-6535. JSTOR 1926560.
- ↑ Merton, R. C. (1971). "Optimum consumption and portfolio rules in a continuous-time model". Journal of Economic Theory 3 (4): 373–413. doi:10.1016/0022-0531(71)90038-X.
- ↑ Bodie, Z.; Merton, R. C.; Samuelson, W. F. (1992). "Labor supply flexibility and portfolio choice in a life cycle model" (PDF). Journal of Economic Dynamics and Control 16 (3–4): 427. doi:10.1016/0165-1889(92)90044-F.
- ↑ Davis, M. H. A.; Norman, A. R. (1990). "Portfolio Selection with Transaction Costs" (PDF). Mathematics of Operations Research 15 (4): 676. doi:10.1287/moor.15.4.676. JSTOR 3689770.
- ↑ Shreve, S. E.; Soner, H. M. (1994). "Optimal Investment and Consumption with Transaction Costs". The Annals of Applied Probability 4 (3): 609. doi:10.1214/aoap/1177004966. JSTOR 2245058.
- ↑ Eastham, J. F.; Hastings, K. J. (1988). "Optimal Impulse Control of Portfolios". Mathematics of Operations Research 13 (4): 588. doi:10.1287/moor.13.4.588. JSTOR 3689945.
- ↑ Schroder, M. (1995). "Optimal Portfolio Selection with Fixed Transaction Costs: Numerical Solutions" (PDF). Working Paper (Michigan State University).
- ↑ Morton, A. J.; Pliska, S. R. (1995). "Optimal Portfolio Management with Fixed Transaction Costs". Mathematical Finance 5 (4): 337. doi:10.1111/j.1467-9965.1995.tb00071.x.
- ↑ http://cmcm.uni-kl.de/fileadmin/downloads/vortraege/20100329/Korn_optimal_portfolios_with_transaction_costs.pdf
- ↑ Karatzas, I.; Lehoczky, J. P.; Sethi, S. P.; Shreve, S. E. (1985). "Explicit solution of a general consumption/investment problem". Stochastic Differential Systems. Lecture Notes in Control and Information Sciences 78. p. 209. doi:10.1007/BFb0041165. ISBN 3-540-16228-3.
- ↑ Sethi, S. P. (1997). "Optimal Consumption and Investment with Bankruptcy". doi:10.1007/978-1-4615-6257-3. ISBN 978-1-4613-7871-6.
- Karatzas, Ioannis; Shreve, Steven E. (1998). "Methods of Mathematical Finance". Stochastic Modelling and Applied Probability 39. doi:10.1007/b98840. ISBN 978-0-387-94839-3.
- Merton R.C.: Continuous Time Finance, Blackwell (1990).
![\max E \left[ \int_0^T e^{-\rho s}u(c_s) \, ds + e^{-\rho T}u(W_T) \right]](../I/m/7c48730f338d73baa0ba0fd54e231d4c.png)
![d W_t = [(r + \pi_t(\mu-r))W_t - c_t ] \, dt +W_t \pi_t \sigma \, dB_t](../I/m/9f1b4b9e9689eb251273ac0ce92f245f.png)