Meredith graph
| Meredith graph | |
|---|---|
|
The Meredith graph | |
| Named after | G. H. Meredith |
| Vertices | 70 |
| Edges | 140 |
| Radius | 7 |
| Diameter | 8 |
| Girth | 4 |
| Automorphisms | 38698352640 |
| Chromatic number | 3 |
| Chromatic index | 5 |
| Properties | Eulerian |
In the mathematical field of graph theory, the Meredith graph is a 4-regular undirected graph with 70 vertices and 140 edges discovered by Guy H. J. Meredith in 1973.[1]
The Meredith graph is 4-vertex-connected and 4-edge-connected, has chromatic number 3, chromatic index 5, radius 7, diameter 8, girth 4 and is non-hamiltonian.[2]
Published in 1973, it provides a counterexample to the Crispin Nash-Williams conjecture that every 4-regular 4-vertex-connected graph is Hamiltonian.[3][4] However, W. T. Tutte showed that all 4-connected planar graphs are hamiltonian.[5]
The characteristic polynomial of the Meredith graph is 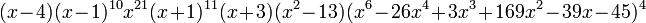 .
.
Gallery
-

The chromatic number of the Meredith graph is 3.
-

The chromatic index of the Meredith graph is 5.
References
- ↑ Weisstein, Eric W., "Meredith graph", MathWorld.
- ↑ Bondy, J. A. and Murty, U. S. R. "Graph Theory". Springer, p. 470, 2007.
- ↑ Meredith, G. H. J. "Regular 4-Valent 4-Connected Nonhamiltonian Non-4-Edge-Colorable Graphs." J. Combin. Th. B 14, 55-60, 1973.
- ↑ Bondy, J. A. and Murty, U. S. R. "Graph Theory with Applications". New York: North Holland, p. 239, 1976.
- ↑ Tutte, W.T., ed., Recent Progress in Combinatorics. Academic Press, New York, 1969.
This article is issued from Wikipedia - version of the Friday, June 26, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
