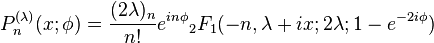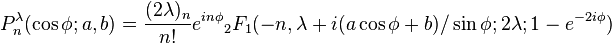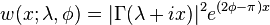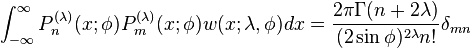Meixner–Pollaczek polynomials
Not to be confused with Meixner polynomials.
In mathematics, the Meixner–Pollaczek polynomials are a family of orthogonal polynomials P(λ)
n(x,φ) introduced by Meixner (1934), which up to elementary changes of variables are the same as the Pollaczek polynomials Pλ
n(x,a,b) rediscovered by Pollaczek (1949) in the case λ=1/2, and later generalized by him.
They are defined by
They are orthogonal on the real line with respect to the weight function
and the orthogonality is given by
See also
References
- Koekoek, Roelof; Lesky, Peter A.; Swarttouw, René F. (2010), Hypergeometric orthogonal polynomials and their q-analogues, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-642-05014-5, ISBN 978-3-642-05013-8, MR 2656096
- Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Pollaczek Polynomials", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
- Meixner, J. (1934), "Orthogonale Polynomsysteme Mit Einer Besonderen Gestalt Der Erzeugenden Funktion", J. London Math. Soc. s1–9: 6–13, doi:10.1112/jlms/s1-9.1.6
- Pollaczek, Félix (1949), "Sur une généralisation des polynomes de Legendre", Les Comptes rendus de l'Académie des sciences 228: 1363–1365, MR 0030037
This article is issued from Wikipedia - version of the Tuesday, March 25, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.