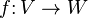Mazur–Ulam theorem

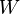In mathematics, the Mazur–Ulam theorem states that if $V$ and $W$ are normed spaces over R and the mapping

f\colon V\to W

is a surjective isometry, then $f$ is affine.

It is named after Stanisław Mazur and Stanislaw Ulam in response to an issue raised by Stefan Banach.

References

Richard J. Fleming; James E. Jamison (2003). Isometries on Banach Spaces: Function Spaces. CRC Press. p. 6. ISBN 1-58488-040-6.
Stanisław Mazur; Stanisław Ulam (1932). "Sur les transformationes isométriques d’espaces vectoriels normés". C. R. Acad. Sci. Paris 194: 946–948.

External links

Jussi Väisälä A proof of the Mazur-Ulam theorem.

This article is issued from Wikipedia - version of the Tuesday, November 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.