Mayo–Lewis equation
The Mayo–Lewis equation or copolymer equation in polymer chemistry describes the distribution of monomers in a copolymer:[1] It is named for Frank R. Mayo and Frederick M. Lewis.
Taking into consideration a monomer mix of two components  and
and 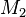 and the four different reactions that can take place at the reactive chain end terminating in either monomer (
and the four different reactions that can take place at the reactive chain end terminating in either monomer ( ) with their reaction rate constants
) with their reaction rate constants  :
:
and with reactivity ratios defined as:
the copolymer equation is given as:
with the concentration of the components given in square brackets. The equation gives the copolymer composition at any instant during the polymerization.
Equation derivation
Monomer 1 is consumed with reaction rate:[2]
![{\frac {-d[M_{1}]}{dt}}=k_{11}[M_{1}]\sum [M_{1}^{*}]+k_{21}[M_{1}]\sum [M_{2}^{*}]\,](../I/m/3dc78c19a18377553151beae43a910e4.png)
with ![\sum [M_{x}^{*}]](../I/m/bbd242d963a5c6db2d1c721018379467.png) the concentration of all the active centers terminating in monomer 1 or 2.
the concentration of all the active centers terminating in monomer 1 or 2.
Likewise the rate of disappearance for monomer 2 is:
![{\frac {-d[M_{2}]}{dt}}=k_{12}[M_{2}]\sum [M_{1}^{*}]+k_{22}[M_{2}]\sum [M_{2}^{*}]\,](../I/m/952fb20206507e18c7409b7b032252bc.png)
Division of both equations yields:
![{\frac {d[M_{1}]}{d[M_{2}]}}={\frac {[M_{1}]}{[M_{2}]}}\left({\frac {k_{11}{\frac {\sum [M_{1}^{*}]}{\sum [M_{2}^{*}]}}+k_{21}}{k_{12}{\frac {\sum [M_{1}^{*}]}{\sum [M_{2}^{*}]}}+k_{22}}}\right)\,](../I/m/72052d769109adc65bfc1f22188ebbe3.png)
The ratio of active center concentrations can be found assuming steady state with:
![{\frac {d\sum [M_{1}^{*}]}{dt}}={\frac {d\sum [M_{2}^{*}]}{dt}}\approx 0\,](../I/m/a0d91130d633c58b23337bfd2ca3b8cb.png)
meaning that the concentration of active centres remains constant, the rate of formation for active center of monomer 1 is equal to the rate of their destruction or:
![k_{21}[M_{1}]\sum [M_{2}^{*}]=k_{12}[M_{2}]\sum [M_{1}^{*}]\,](../I/m/166df310517c5eacaedeb43162a032f2.png)
or
![{\frac {\sum [M_{1}^{*}]}{\sum [M_{2}^{*}]}}={\frac {k_{21}[M_{1}]}{k_{12}[M_{2}]}}\,](../I/m/9dc9c686459d79d062be7dcd0a3d339b.png)
Substituting into the ratio of monomer consumption rates eliminates the radical concentrations and yields the Mayo-Lewis equation.
Instantaneous form
It can often be useful to alter the copolymer equation by expressing concentration in terms of mole fractions. Mole fractions of monomers  and
and 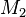 in the feed are defined as
in the feed are defined as 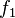 and
and  where
where

Similarly,  represents the mole fraction of each monomer in the copolymer:
represents the mole fraction of each monomer in the copolymer:

These equations can be combined with the Mayo-Lewis Equation to give
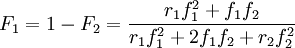
This equation gives the instantaneous copolymer composition. It is important to note that the feed and copolymer compositions can change as polymerization proceeds.
Limiting cases
Reactivity ratios indicate preference for propagation. Large  indicates a tendency for
indicates a tendency for 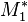 to add
to add  , while small values indicate a tendency for
, while small values indicate a tendency for 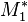 to add
to add 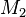 . From the definition of reactivity ratios, several special cases can be derived:
. From the definition of reactivity ratios, several special cases can be derived:
-
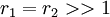 with both reactivity ratios very high the two monomers only react with themselves and not each other leading to a mixture of two homopolymers.
with both reactivity ratios very high the two monomers only react with themselves and not each other leading to a mixture of two homopolymers. -
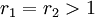 with both ratios larger than 1, homopolymerization of component M_1 is favored but in the event of a crosspolymerization by M_2 the chain-end will continue giving rise to block copolymer
with both ratios larger than 1, homopolymerization of component M_1 is favored but in the event of a crosspolymerization by M_2 the chain-end will continue giving rise to block copolymer -
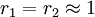 with both ratios around 1, monomer 1 will react as fast with another monomer 1 or monomer 2 and a random copolymer is formed.
with both ratios around 1, monomer 1 will react as fast with another monomer 1 or monomer 2 and a random copolymer is formed. -
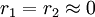 with both values approaching 0 the monomers are unable to homopolymerize and only add each other resulting in an alternating polymer
with both values approaching 0 the monomers are unable to homopolymerize and only add each other resulting in an alternating polymer -
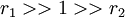 In the initial stage of the copolymerization monomer 1 is incorporated faster and the copolymer is rich in monomer 1. When this monomer gets depleted, more monomer 2 segments are added. This is called composition drift.
In the initial stage of the copolymerization monomer 1 is incorporated faster and the copolymer is rich in monomer 1. When this monomer gets depleted, more monomer 2 segments are added. This is called composition drift.
An example case is maleic anhydride and styrene, with reactivity ratios:
- Maleic anhydride (
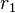 = 0.01) & styrene (
= 0.01) & styrene (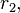 = 0.02)[3]
= 0.02)[3]
Neither of these compounds homopolymerize and instead they react together to give almost exclusively alternating copolymer.
When both 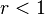 , the system has an azeotrope, where feed and copolymer composition are the same.
, the system has an azeotrope, where feed and copolymer composition are the same.
Calculation of reactivity ratios
Calculation of reactivity ratios generally involves carrying out several polymerizations at varying monomer ratios. The copolymer composition can be analysed with methods such as Proton nuclear magnetic resonance, Carbon-13 nuclear magnetic resonance, or Fourier transform infrared spectroscopy. The polymerizations are also carried out at low conversions, so monomer concentrations can be assumed to be constant. With all the other parameters in the copolymer equation known, 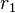 and
and 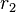 can be found.
can be found.
Curve Fitting
One of the simplest methods for finding reactivity ratios is plotting the copolymer equation and using least squares analysis to find the 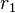 ,
, 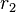 pair that gives the best fit curve.
pair that gives the best fit curve.
Mayo-Lewis Method
The Mayo-Lewis method uses a form of the copolymer equation relating 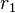 to
to 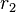 :[4]
:[4]
![r_{1}={\frac {f_{1}}{f_{2}}}\left[{\frac {F_{2}}{F_{1}}}(1+{\frac {f_{1}r_{1}}{f_{2}}})-1\right]\,](../I/m/ae737d3b95320ba03caa0d9f3b9dc7cf.png)
For each different monomer composition, a line is generated using arbitrary 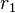 values. The intersection of these lines is the
values. The intersection of these lines is the 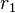 ,
, 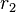 for the system. More frequently, the lines do not intersect and the area in which most line intersect can be given as a range of
for the system. More frequently, the lines do not intersect and the area in which most line intersect can be given as a range of 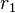 , and
, and 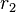 values.
values.
Fineman-Ross Method
Fineman and Ross rearranged the copolymer equation into a linear form:[5]

where 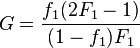 and
and ![H=\left[{\frac {f_{1}^{2}(1-F_{1})}{(1-f_{1})^{2}F_{1}}}\right]\,](../I/m/02bff3551282166c897532102d742d39.png) .
.
Thus, a plot of  versus
versus 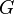 yields a straight line with slope
yields a straight line with slope 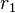 and intercept
and intercept 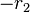
Kelen Tudos method
The Fineman-Ross method can be biased towards points at low or high monomer concentration, so Kelen and Tudos introduced and arbitrary constant,
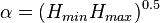
where 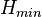 and
and 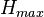 are the highest and lowest values of
are the highest and lowest values of  from the Fineman-Ross method.[6] The data can be plotted in a linear form
from the Fineman-Ross method.[6] The data can be plotted in a linear form
![\eta =\left[r_{1}+{\frac {r_{2}}{\alpha }}\right]\mu -{\frac {r_{2}}{\alpha }}\,](../I/m/0b248ae851eadbf751a6d01b42a9c218.png)
where  and
and  . Plotting
. Plotting  against
against 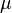 yields a straight line that gives
yields a straight line that gives 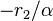 when
when  and
and 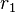 when
when 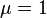 . This distributes the data more symmetrically and can yield better results.
. This distributes the data more symmetrically and can yield better results.
Q-e scheme
A semi-empirical method for the determination of reactivity ratios is called the Q-e scheme. This involves using two parameters for each monomer, 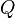 and
and  . The reaction of
. The reaction of 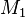 radical with
radical with  monomer is written as
monomer is written as
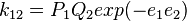
while the reaction of 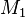 radical with
radical with 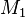 monomer is written as
monomer is written as

Using these definitions 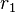 and
and  can be found by the ratio of the terms. An advantage of this system is that reactivity ratios can be found using tabulated Q-e values of monomers regardless or what the monomer pair is in the system.
can be found by the ratio of the terms. An advantage of this system is that reactivity ratios can be found using tabulated Q-e values of monomers regardless or what the monomer pair is in the system.
External links
References
- ↑ Copolymerization. I. A Basis for Comparing the Behavior of Monomers in Copolymerization; The Copolymerization of Styrene and Methyl Methacrylate Frank R. Mayo and Frederick M. Lewis J. Am. Chem. Soc.; 1944; 66(9) pp 1594 - 1601; doi:10.1021/ja01237a052
- ↑ Young, Robert J. (1983). Introduction to polymers ([Reprinted with additional material] ed.). London: Chapman and Hall. ISBN 0-412-22170-5.
- ↑ Copolymer Reactivity Ratios. Polymer Handbook, 4th ed,; Wiley, 2003; Vol 1, pp 259.
- ↑ Mayo, F. R.; Lewis, F. M. J. Am. Chem. Soc. 1944, 66, 1594.
- ↑ Fineman, M.; Ross, S. D. J. Polymer Sci. 1950, 5, 259.
- ↑ Kelen, T.; Tudos, F.; Turcsanyi, B. Polymer Bull. 1980, 2, 71-76.

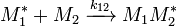
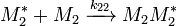
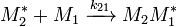
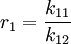
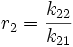
![{\frac {d\left[M_{1}\right]}{d\left[M_{2}\right]}}={\frac {\left[M_{1}\right]\left(r_{1}\left[M_{1}\right]+\left[M_{2}\right]\right)}{\left[M_{2}\right]\left(\left[M_{1}\right]+r_{2}\left[M_{2}\right]\right)}}](../I/m/dea8c560dd0363f25dc92f414a5b64f6.png)