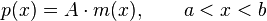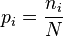Principle of maximum entropy
The principle of maximum entropy states that, subject to precisely stated prior data (such as a proposition that expresses testable information), the probability distribution which best represents the current state of knowledge is the one with largest entropy.
Another way of stating this: Take precisely stated prior data or testable information about a probability distribution function. Consider the set of all trial probability distributions that would encode the prior data. Of those, the one with maximal information entropy is the proper distribution, according to this principle.
History
The principle was first expounded by E. T. Jaynes in two papers in 1957[1][2] where he emphasized a natural correspondence between statistical mechanics and information theory. In particular, Jaynes offered a new and very general rationale why the Gibbsian method of statistical mechanics works. He argued that the entropy of statistical mechanics and the information entropy of information theory are principally the same thing. Consequently, statistical mechanics should be seen just as a particular application of a general tool of logical inference and information theory.
Overview
In most practical cases, the stated prior data or testable information is given by a set of conserved quantities (average values of some moment functions), associated with the probability distribution in question. This is the way the maximum entropy principle is most often used in statistical thermodynamics. Another possibility is to prescribe some symmetries of the probability distribution. The equivalence between conserved quantities and corresponding symmetry groups implies a similar equivalence for these two ways of specifying the testable information in the maximum entropy method.
The maximum entropy principle is also needed to guarantee the uniqueness and consistency of probability assignments obtained by different methods, statistical mechanics and logical inference in particular.
The maximum entropy principle makes explicit our freedom in using different forms of prior data. As a special case, a uniform prior probability density (Laplace's principle of indifference, sometimes called the principle of insufficient reason), may be adopted. Thus, the maximum entropy principle is not merely an alternative way to view the usual methods of inference of classical statistics, but represents a significant conceptual generalization of those methods. It means that thermodynamics systems need not be shown to be ergodic to justify treatment as a statistical ensemble.
In ordinary language, the principle of maximum entropy can be said to express a claim of epistemic modesty, or of maximum ignorance. The selected distribution is the one that makes the least claim to being informed beyond the stated prior data, that is to say the one that admits the most ignorance beyond the stated prior data.
Testable information
The principle of maximum entropy is useful explicitly only when applied to testable information. Testable information is a statement about a probability distribution whose truth or falsity is well-defined. For example, the statements
- the expectation of the variable x is 2.87
and
- p2 + p3 > 0.6
(where p2 + p3 are probabilities of events) are statements of testable information.
Given testable information, the maximum entropy procedure consists of seeking the probability distribution which maximizes information entropy, subject to the constraints of the information. This constrained optimization problem is typically solved using the method of Lagrange multipliers.
Entropy maximization with no testable information respects the universal "constraint" that the sum of the probabilities is one. Under this constraint, the maximum entropy discrete probability distribution is the uniform distribution,
Applications
The principle of maximum entropy is commonly applied in two ways to inferential problems:
Prior probabilities
The principle of maximum entropy is often used to obtain prior probability distributions for Bayesian inference. Jaynes was a strong advocate of this approach, claiming the maximum entropy distribution represented the least informative distribution.[3] A large amount of literature is now dedicated to the elicitation of maximum entropy priors and links with channel coding.[4][5][6][7]
Maximum entropy models
Alternatively, the principle is often invoked for model specification: in this case the observed data itself is assumed to be the testable information. Such models are widely used in natural language processing. An example of such a model is logistic regression, which corresponds to the maximum entropy classifier for independent observations.
General solution for the maximum entropy distribution with linear constraints
Discrete case
We have some testable information I about a quantity x taking values in {x1, x2,..., xn}. We assume this information has the form of m constraints on the expectations of the functions fk; that is, we require our probability distribution to satisfy
Furthermore, the probabilities must sum to one, giving the constraint
The probability distribution with maximum information entropy subject to these constraints is
It is sometimes called the Gibbs distribution. The normalization constant is determined by
and is conventionally called the partition function. (Interestingly, the Pitman–Koopman theorem states that the necessary and sufficient condition for a sampling distribution to admit sufficient statistics of bounded dimension is that it have the general form of a maximum entropy distribution.)
The λk parameters are Lagrange multipliers whose particular values are determined by the constraints according to
These m simultaneous equations do not generally possess a closed form solution, and are usually solved by numerical methods.
Continuous case
For continuous distributions, the Shannon entropy cannot be used, as it is only defined for discrete probability spaces. Instead Edwin Jaynes (1963, 1968, 2003) gave the following formula, which is closely related to the relative entropy (see also differential entropy).
where m(x), which Jaynes called the "invariant measure", is proportional to the limiting density of discrete points. For now, we shall assume that m is known; we will discuss it further after the solution equations are given.
A closely related quantity, the relative entropy, is usually defined as the Kullback–Leibler divergence of m from p (although it is sometimes, confusingly, defined as the negative of this). The inference principle of minimizing this, due to Kullback, is known as the Principle of Minimum Discrimination Information.
We have some testable information I about a quantity x which takes values in some interval of the real numbers (all integrals below are over this interval). We assume this information has the form of m constraints on the expectations of the functions fk, i.e. we require our probability density function to satisfy
And of course, the probability density must integrate to one, giving the constraint
The probability density function with maximum Hc subject to these constraints is
with the partition function determined by
As in the discrete case, the values of the  parameters are determined by the constraints according to
parameters are determined by the constraints according to
The invariant measure function m(x) can be best understood by supposing that x is known to take values only in the bounded interval (a, b), and that no other information is given. Then the maximum entropy probability density function is
where A is a normalization constant. The invariant measure function is actually the prior density function encoding 'lack of relevant information'. It cannot be determined by the principle of maximum entropy, and must be determined by some other logical method, such as the principle of transformation groups or marginalization theory.
Examples
For several examples of maximum entropy distributions, see the article on maximum entropy probability distributions.
Justifications for the principle of maximum entropy
Proponents of the principle of maximum entropy justify its use in assigning probabilities in several ways, including the following two arguments. These arguments take the use of Bayesian probability as given, and are thus subject to the same postulates.
Information entropy as a measure of 'uninformativeness'
Consider a discrete probability distribution among m mutually exclusive propositions. The most informative distribution would occur when one of the propositions was known to be true. In that case, the information entropy would be equal to zero. The least informative distribution would occur when there is no reason to favor any one of the propositions over the others. In that case, the only reasonable probability distribution would be uniform, and then the information entropy would be equal to its maximum possible value, log m. The information entropy can therefore be seen as a numerical measure which describes how uninformative a particular probability distribution is, ranging from zero (completely informative) to log m (completely uninformative).
By choosing to use the distribution with the maximum entropy allowed by our information, the argument goes, we are choosing the most uninformative distribution possible. To choose a distribution with lower entropy would be to assume information we do not possess. Thus the maximum entropy distribution is the only reasonable distribution.
The Wallis derivation
The following argument is the result of a suggestion made by Graham Wallis to E. T. Jaynes in 1962.[8] It is essentially the same mathematical argument used for the Maxwell–Boltzmann statistics in statistical mechanics, although the conceptual emphasis is quite different. It has the advantage of being strictly combinatorial in nature, making no reference to information entropy as a measure of 'uncertainty', 'uninformativeness', or any other imprecisely defined concept. The information entropy function is not assumed a priori, but rather is found in the course of the argument; and the argument leads naturally to the procedure of maximizing the information entropy, rather than treating it in some other way.
Suppose an individual wishes to make a probability assignment among m mutually exclusive propositions. She has some testable information, but is not sure how to go about including this information in her probability assessment. She therefore conceives of the following random experiment. She will distribute N quanta of probability (each worth 1/N) at random among the m possibilities. (One might imagine that she will throw N balls into m buckets while blindfolded. In order to be as fair as possible, each throw is to be independent of any other, and every bucket is to be the same size.) Once the experiment is done, she will check if the probability assignment thus obtained is consistent with her information. (For this step to be successful, the information must be a constraint given by an open set in the space of probability measures). If it is inconsistent, she will reject it and try again. If it is consistent, her assessment will be
where pi is the probability of the ith proposition, while ni is the number of quanta that were assigned to the ith proposition (i.e. the number of balls that ended up in bucket i).
Now, in order to reduce the 'graininess' of the probability assignment, it will be necessary to use quite a large number of quanta of probability. Rather than actually carry out, and possibly have to repeat, the rather long random experiment, the protagonist decides to simply calculate and use the most probable result. The probability of any particular result is the multinomial distribution,
where
is sometimes known as the multiplicity of the outcome.
The most probable result is the one which maximizes the multiplicity W. Rather than maximizing W directly, the protagonist could equivalently maximize any monotonic increasing function of W. She decides to maximize
At this point, in order to simplify the expression, the protagonist takes the limit as  , i.e. as the probability levels go from grainy discrete values to smooth continuous values. Using Stirling's approximation, she finds
, i.e. as the probability levels go from grainy discrete values to smooth continuous values. Using Stirling's approximation, she finds
All that remains for the protagonist to do is to maximize entropy under the constraints of her testable information. She has found that the maximum entropy distribution is the most probable of all "fair" random distributions, in the limit as the probability levels go from discrete to continuous.
Compatibility with Bayes' theorem
Giffin and Caticha (2007) state that Bayes' theorem and the principle of maximum entropy are completely compatible and can be seen as special cases of the "method of maximum relative entropy". They state that this method reproduces every aspect of orthodox Bayesian inference methods. In addition this new method opens the door to tackling problems that could not be addressed by either the maximal entropy principle or orthodox Bayesian methods individually. Moreover, recent contributions (Lazar 2003, and Schennach 2005) show that frequentist relative-entropy-based inference approaches (such as empirical likelihood and exponentially tilted empirical likelihood - see e.g. Owen 2001 and Kitamura 2006) can be combined with prior information to perform Bayesian posterior analysis.
Jaynes stated Bayes' theorem was a way to calculate a probability, while maximum entropy was a way to assign a prior probability distribution.[9]
It is however, possible in concept to solve for a posterior distribution directly from a stated prior distribution using the Principle of Minimum Cross Entropy (or the Principle of Maximum Entropy being a special case of using a uniform distribution as the given prior), independently of any Bayesian considerations by treating the problem formally as a constrained optimisation problem, the Entropy functional being the objective function. For the case of given average values as testable information (averaged over the sought after probability distribution), the sought after distribution is formally the Gibbs (or Boltzmann) distribution the parameters of which must be solved for in order to achieve minimum cross entropy and satisfy the given testable information.
See also
- Akaike information criterion
- Dissipation
- Entropy maximization
- Maximum entropy classifier
- Maximum entropy probability distribution
- Maximum entropy spectral estimation
- Maximum entropy thermodynamics
Notes
- ↑ Jaynes, E. T. (1957). "Information Theory and Statistical Mechanics" (PDF). Physical Review. Series II 106 (4): 620–630. Bibcode:1957PhRv..106..620J. doi:10.1103/PhysRev.106.620. MR 87305.
- ↑ Jaynes, E. T. (1957). "Information Theory and Statistical Mechanics II" (PDF). Physical Review. Series II 108 (2): 171–190. Bibcode:1957PhRv..108..171J. doi:10.1103/PhysRev.108.171. MR 96414.
- ↑ Jaynes, E. T. (1968). "Prior Probabilities" (PDF or PostScript). IEEE Transactions on Systems Science and Cybernetics 4 (3): 227–241. doi:10.1109/TSSC.1968.300117.
- ↑ Clarke, B. (2006). "Information optimality and Bayesian modelling". Journal of Econometrics 138 (2): 405–429. doi:10.1016/j.jeconom.2006.05.003.
- ↑ Soofi, E.S. (2000). "Principal Information Theoretic Approaches". Journal of the American Statistical Association 95 (452): 1349–1353. doi:10.2307/2669786. JSTOR 2669786. MR 1825292.
- ↑ Bousquet, N. (2008). "Eliciting vague but proper maximal entropy priors in Bayesian experiments". Statistical Papers 51 (3): 613–628. doi:10.1007/s00362-008-0149-9.
- ↑ Palmieri, Francesco A. N.; Ciuonzo, Domenico (2013-04-01). "Objective priors from maximum entropy in data classification". Information Fusion 14 (2): 186–198. doi:10.1016/j.inffus.2012.01.012.
- ↑ Jaynes, E. T. (2003) Probability Theory: The Logic of Science, Cambridge University Press, p. 351-355. ISBN 978-0521592710
- ↑ Jaynes, E. T. (1988) "The Relation of Bayesian and Maximum Entropy Methods", in Maximum-Entropy and Bayesian Methods in Science and Engineering (Vol. 1), Kluwer Academic Publishers, p. 25-29.
References
- Jaynes, E. T. (1963). "Information Theory and Statistical Mechanics". In Ford, K. (ed.). Statistical Physics. New York: Benjamin. p. 181.
- Jaynes, E. T., 1986 (new version online 1996),
 , in Maximum-Entropy and Bayesian Methods in Applied Statistics, J. H. Justice (ed.), Cambridge University Press, Cambridge, p. 26.
, in Maximum-Entropy and Bayesian Methods in Applied Statistics, J. H. Justice (ed.), Cambridge University Press, Cambridge, p. 26. - Bajkova, A. T., 1992, The generalization of maximum entropy method for reconstruction of complex functions. Astronomical and Astrophysical Transactions, V.1, issue 4, p. 313-320.
- Giffin, A. and Caticha, A., 2007, Updating Probabilities with Data and Moments
- Guiasu, S. and Shenitzer, A., 1985, 'The principle of maximum entropy', The Mathematical Intelligencer, 7(1), 42-48.
- Harremoës P. and Topsøe F., 2001, Maximum Entropy Fundamentals, Entropy, 3(3), 191-226.
- Kapur, J. N.; and Kesavan, H. K., 1992, Entropy optimization principles with applications, Boston: Academic Press. ISBN 0-12-397670-7
- Kitamura, Y., 2006, Empirical Likelihood Methods in Econometrics: Theory and Practice, Cowles Foundation Discussion Papers 1569, Cowles Foundation, Yale University.
- Lazar, N., 2003, "Bayesian Empirical Likelihood", Biometrika, 90, 319-326.
- Owen, A. B., Empirical Likelihood, Chapman and Hall.
- Schennach, S. M., 2005, "Bayesian Exponentially Tilted Empirical Likelihood", Biometrika, 92(1), 31-46.
- Uffink, Jos, 1995, 'Can the Maximum Entropy Principle be explained as a consistency requirement?', Studies in History and Philosophy of Modern Physics 26B, 223-261.
Further reading
- Ratnaparkhi A. (1997) "A simple introduction to maximum entropy models for natural language processing" Technical Report 97-08, Institute for Research in Cognitive Science, University of Pennsylvania. An easy-to-read introduction to maximum entropy methods in the context of natural language processing.
- Tang, A.; Jackson, D.; Hobbs, J.; Chen, W.; Smith, J. L.; Patel, H.; Prieto, A.; Petrusca, D.; Grivich, M. I.; Sher, A.; Hottowy, P.; Dabrowski, W.; Litke, A. M.; Beggs, J. M. (2008). "A Maximum Entropy Model Applied to Spatial and Temporal Correlations from Cortical Networks in Vitro". Journal of Neuroscience 28 (2): 505–518. doi:10.1523/JNEUROSCI.3359-07.2008. PMID 18184793. Open access article containing pointers to various papers and software implementations of Maximum Entropy Model on the net.
External links
- Maximum Entropy Modeling Links to publications, software and resources
- MaxEnt and Exponential Models Links to pedagogically-oriented material on maximum entropy and exponential models


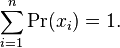
![\Pr(x_i) = \frac{1}{Z(\lambda_1,\ldots, \lambda_m)} \exp\left[\lambda_1 f_1(x_i) + \cdots + \lambda_m f_m(x_i)\right].](../I/m/8f8e0acc69e4e25af4154f8b11d29a0f.png)
![Z(\lambda_1,\ldots, \lambda_m) = \sum_{i=1}^n \exp\left[\lambda_1 f_1(x_i) + \cdots + \lambda_m f_m(x_i)\right],](../I/m/77ad132fab67679491936e6050035aa5.png)




![p(x) = \frac{1}{Z(\lambda_1,\dotsc, \lambda_m)} m(x)\exp\left[\lambda_1 f_1(x) + \dotsb + \lambda_m f_m(x)\right]](../I/m/c5d51c83dc638209d7f8ee8f2a705716.png)
![Z(\lambda_1,\dotsc, \lambda_m) = \int m(x)\exp\left[\lambda_1 f_1(x) + \dotsb + \lambda_m f_m(x)\right]dx.](../I/m/551da0ebb3dd98304d0ab8ef00d25197.png)