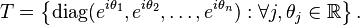Maximal torus

In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.

A torus in a compact Lie group G is a compact, connected, abelian Lie subgroup of G (and therefore isomorphic to the standard torus Tⁿ). A maximal torus is one which is maximal among such subgroups. That is, T is a maximal torus if for any other torus T′ containing T we have T = T′. Every torus is contained in a maximal torus simply by dimensional considerations. A noncompact Lie group need not have any nontrivial tori (e.g. Rⁿ).

The dimension of a maximal torus in G is called the rank of G. The rank is well-defined since all maximal tori turn out to be conjugate. For semisimple groups the rank is equal to the number of nodes in the associated Dynkin diagram.

Examples

The unitary group U(n) has as a maximal torus the subgroup of all diagonal matrices. That is,

T = \left\{\mathrm{diag}(e^{i\theta_1},e^{i\theta_2},\dots,e^{i\theta_n}) : \forall j, \theta_j \in \mathbb R\right\}.

T is clearly isomorphic to the product of n circles, so the unitary group U(n) has rank n. A maximal torus in the special unitary group SU(n) ⊂ U(n) is just the intersection of T and SU(n) which is a torus of dimension n − 1.

A maximal torus in the special orthogonal group SO(2n) is given by the set of all simultaneous rotations in any fixed choice of n pairwise orthogonal 2-planes. This is also a maximal torus in the group SO(2n+1) where the action fixes the remaining direction. Thus both SO(2n) and SO(2n+1) have rank n. For example, in the rotation group SO(3) the maximal tori are given by rotations about a fixed axis.

The symplectic group Sp(n) has rank n. A maximal torus is given by the set of all diagonal matrices whose entries all lie in a fixed complex subalgebra of H.

Properties

Let G be a compact, connected Lie group and let 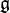$\mathfrak g$ be the Lie algebra of G.

A maximal torus in G is a maximal abelian subgroup, but the converse need not hold.
The maximal tori in G are exactly the Lie subgroups corresponding to the maximal abelian, diagonally acting subalgebras of 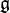$\mathfrak g$ (cf. Cartan subalgebra)
Given a maximal torus T in G, every element g ∈ G is conjugate to an element in T.^[1]
Since the conjugate of a maximal torus is a maximal torus, every element of G lies in some maximal torus.
All maximal tori in G are conjugate.^[2] Therefore, the maximal tori form a single conjugacy class among the subgroups of G.
It follows that the dimensions of all maximal tori are the same. This dimension is the rank of G.
If G has dimension n and rank r then n − r is even.

Weyl group

Given a torus T (not necessarily maximal), the Weyl group of G with respect to T can be defined as the normalizer of T modulo the centralizer of T. That is, 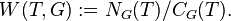$W(T,G) := N_G(T)/C_G(T).$ Fix a maximal torus 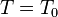$T = T_0$ in G; then the corresponding Weyl group is called the Weyl group of G (it depends up to isomorphism on the choice of T). The representation theory of G is essentially determined by T and W.

The Weyl group acts by (outer) automorphisms on T (and its Lie algebra).
The centralizer of T in G is equal to T, so the Weyl group is equal to N(T)/T.
The identity component of the normalizer of T is also equal to T. The Weyl group is therefore equal to the component group of N(T).
The normalizer of T is closed, so the Weyl group is finite
Two elements in T are conjugate if and only if they are conjugate by an element of W. That is, the conjugacy classes of G intersect T in a Weyl orbit.
The space of conjugacy classes in G is homeomorphic to the orbit space T/W and, if f is a continuous function on G invariant under conjugation, the Weyl integration formula holds:

\displaystyle{\int_G f(g)\, dg = |W|^{-1} \int_T f(t) |\Delta(t)|^2\, dt,}

where Δ is given by the Weyl denominator formula.

References

↑ Hall 2015 Theorem 11.9.
↑ Hall 2015 Theorem 11.9

Adams, J. F. (1969), Lectures on Lie Groups, University of Chicago Press, ISBN 0226005305
Bourbaki, N. (1982), Groupes et Algèbres de Lie (Chapitre 9), Éléments de Mathématique, Masson, ISBN 354034392X
Dieudonné, J. (1977), Compact Lie groups and semisimple Lie groups, Chapter XXI, Treatise on analysis 5, Academic Press, ISBN 012215505X
Duistermaat, J.J.; Kolk, A. (2000), Lie groups, Universitext, Springer, ISBN 3540152938
Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics 222 (2nd ed.), Springer
Helgason, Sigurdur (1978), Differential geometry, Lie groups, and symmetric spaces, Academic Press, ISBN 0821828487
Hochschild, G. (1965), The structure of Lie groups, Holden-Day

This article is issued from Wikipedia - version of the Saturday, February 13, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Maximal torus

Examples

Properties

Weyl group

See also

References