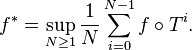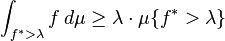Maximal ergodic theorem

The maximal ergodic theorem is a theorem in ergodic theory, a discipline within mathematics.

Suppose that 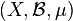$(X, \mathcal{B},\mu)$ is a probability space, that 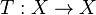$T : X\to X$ is a (possibly noninvertible) measure-preserving transformation, and that 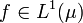$f\in L^1(\mu)$ . Define $f^*$ by

f^* = \sup_{N\geq 1} \frac{1}{N} \sum_{i=0}^{N-1} f \circ T^i.

Then the maximal ergodic theorem states that

\int_{f^{*} > \lambda} f \, d\mu \ge \lambda \cdot \mu\{ f^{*} > \lambda\}

for any λ ∈ R.

This theorem is used to prove the point-wise ergodic theorem.

References

Keane, Michael; Petersen, Karl (2006), "Easy and nearly simultaneous proofs of the Ergodic Theorem and Maximal Ergodic Theorem", Institute of Mathematical Statistics Lecture Notes - Monograph Series, Institute of Mathematical Statistics Lecture Notes - Monograph Series 48: 248–251, doi:10.1214/074921706000000266, ISBN 0-940600-64-1 .

This article is issued from Wikipedia - version of the Tuesday, March 03, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.