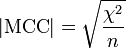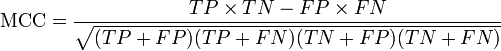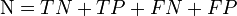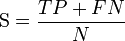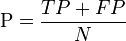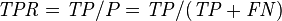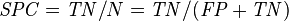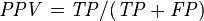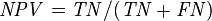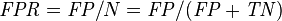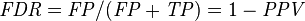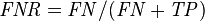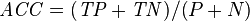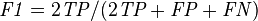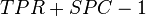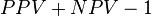Matthews correlation coefficient

The Matthews correlation coefficient is used in machine learning as a measure of the quality of binary (two-class) classifications, introduced by biochemist Brian W. Matthews in 1975.[1] It takes into account true and false positives and negatives and is generally regarded as a balanced measure which can be used even if the classes are of very different sizes. The MCC is in essence a correlation coefficient between the observed and predicted binary classifications; it returns a value between −1 and +1. A coefficient of +1 represents a perfect prediction, 0 no better than random prediction and −1 indicates total disagreement between prediction and observation. The statistic is also known as the phi coefficient. MCC is related to the chi-square statistic for a 2×2 contingency table

|\text{MCC}| = \sqrt{\frac{\chi^2}{n}}

where n is the total number of observations.

While there is no perfect way of describing the confusion matrix of true and false positives and negatives by a single number, the Matthews correlation coefficient is generally regarded as being one of the best such measures.[2] Other measures, such as the proportion of correct predictions (also termed accuracy), are not useful when the two classes are of very different sizes. For example, assigning every object to the larger set achieves a high proportion of correct predictions, but is not generally a useful classification.

The MCC can be calculated directly from the confusion matrix using the formula:

\text{MCC} = \frac{ TP \times TN - FP \times FN } {\sqrt{ (TP + FP) ( TP + FN ) ( TN + FP ) ( TN + FN ) } }

In this equation, TP is the number of true positives, TN the number of true negatives, FP the number of false positives and FN the number of false negatives. If any of the four sums in the denominator is zero, the denominator can be arbitrarily set to one; this results in a Matthews correlation coefficient of zero, which can be shown to be the correct limiting value.

The original formula as given by Matthews was:[1]

\text{N} = TN + TP + FN + FP
\text{S} = \frac{ TP + FN } { N }
\text{P} = \frac{ TP + FP } { N }
\text{MCC} = \frac{ TP / N - S \times P } {\sqrt{ P S ( 1 - S) ( 1 - P ) } }

This is equal to the formula given above. As a correlation coefficient, the Matthews correlation coefficient is the geometric mean of the regression coefficients of the problem and its dual. The component regression coefficients of the Matthews correlation coefficient are Markedness (deltap) and Youden's J statistic (Informedness or deltap').[2][3] Markedness and Informedness correspond to different directions of information flow and generalize Youden's J statistic, the deltap statistics and (as their geometric mean) the Matthews Correlation Coefficient to more than two classes.[2]

Confusion Matrix

Main article: Confusion matrix
Terminology and derivations
from a confusion matrix
true positive (TP)
eqv. with hit
true negative (TN)
eqv. with correct rejection
false positive (FP)
eqv. with false alarm, Type I error
false negative (FN)
eqv. with miss, Type II error
sensitivity or true positive rate (TPR)
eqv. with hit rate, recall
\mathit{TPR} = \mathit{TP} / P = \mathit{TP} / (\mathit{TP}+\mathit{FN})
specificity (SPC) or True Negative Rate
\mathit{SPC} = \mathit{TN} / N = \mathit{TN} / (\mathit{FP} + \mathit{TN})
precision or positive predictive value (PPV)
\mathit{PPV} = \mathit{TP} / (\mathit{TP} + \mathit{FP})
negative predictive value (NPV)
\mathit{NPV} = \mathit{TN} / (\mathit{TN} + \mathit{FN})
fall-out or false positive rate (FPR)
\mathit{FPR} = \mathit{FP} / N = \mathit{FP} / (\mathit{FP} + \mathit{TN})
false discovery rate (FDR)
\mathit{FDR} = \mathit{FP} / (\mathit{FP} + \mathit{TP}) = 1 - \mathit{PPV}
Miss Rate or False Negative Rate (FNR)
\mathit{FNR} = \mathit{FN} / (\mathit{FN} + \mathit{TP})
accuracy (ACC)
\mathit{ACC} = (\mathit{TP} + \mathit{TN}) / (P + N)
F1 score
is the harmonic mean of precision and sensitivity
\mathit{F1} = 2 \mathit{TP} / (2 \mathit{TP} + \mathit{FP} + \mathit{FN})
Matthews correlation coefficient (MCC)
\frac{ TP \times TN - FP \times FN } {\sqrt{ (TP+FP) ( TP + FN ) ( TN + FP ) ( TN + FN ) } }
Informedness
TPR + SPC - 1
Markedness
PPV + NPV - 1

Sources: Fawcett (2006) and Powers (2011).[2][4]

Let us define an experiment from P positive instances and N negative instances for some condition. The four outcomes can be formulated in a 2×2 contingency table or confusion matrix, as follows:

True condition
Total population Condition positive Condition negative Prevalence = Σ Condition positive/Σ Total population
Predicted
condition		 Predicted condition
positive		 True positive False positive
(Type I error)		 Positive predictive value (PPV), Precision = Σ True positive/Σ Test outcome positive False discovery rate (FDR) = Σ False positive/Σ Test outcome positive
Predicted condition
negative		 False negative
(Type II error)		 True negative False omission rate (FOR) = Σ False negative/Σ Test outcome negative Negative predictive value (NPV) = Σ True negative/Σ Test outcome negative
Accuracy (ACC) = Σ True positive + Σ True negative/Σ Total population True positive rate (TPR), Sensitivity, Recall = Σ True positive/Σ Condition positive False positive rate (FPR), Fall-out = Σ False positive/Σ Condition negative Positive likelihood ratio (LR+) = TPR/FPR Diagnostic odds ratio (DOR) = LR+/LR−
False negative rate (FNR), Miss rate = Σ False negative/Σ Condition positive True negative rate (TNR), Specificity (SPC) = Σ True negative/Σ Condition negative Negative likelihood ratio (LR−) = FNR/TNR

See also

References

  1. 1 2 Matthews, B. W. (1975). "Comparison of the predicted and observed secondary structure of T4 phage lysozyme". Biochimica et Biophysica Acta (BBA) - Protein Structure 405 (2): 442–451. doi:10.1016/0005-2795(75)90109-9.
  2. 1 2 3 4 Powers, David M W (2011). "Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation" (PDF). Journal of Machine Learning Technologies 2 (1): 37–63.
  3. ↑ Perruchet, P.; Peereman, R. (2004). "The exploitation of distributional information in syllable processing". J. Neurolinguistics 17: 97–119. doi:10.1016/s0911-6044(03)00059-9.
  4. ↑ Fawcelt, Tom (2006). "An Introduction to ROC Analysis". Pattern Recognition Letters 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010.


This article is issued from Wikipedia - version of the Wednesday, February 10, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.