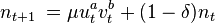Matching theory (economics)
In economics, matching theory, also known as search and matching theory, is a mathematical framework attempting to describe the formation of mutually beneficial relationships over time.
Matching theory has been especially influential in labor economics, where it has been used to describe the formation of new jobs, as well as to describe other human relationships like marriage. Matching theory evolved from an earlier framework called 'search theory'. Where search theory studies the microeconomic decision of an individual searcher, matching theory studies the macroeconomic outcome when one or more types of searchers interact. It offers a way of modeling markets in which frictions prevent instantaneous adjustment of the level of economic activity. Among other applications, it has been used as a framework for studying frictional unemployment.
One of the founders of matching theory is Dale T. Mortensen of Northwestern University. A textbook treatment of the matching approach to labor markets is Christopher A. Pissarides' book Equilibrium Unemployment Theory.[1] Mortensen and Pissarides, together with Peter A. Diamond, were awarded the 2010 Nobel Prize in Economics for 'fundamental contributions to search and matching theory'.[2] The 2012 Economic Prize Committee of the Royal Swedish Academy of Sciences was awarded to Alvin E. Roth and Lloyd Shapley for their work on matching theory.[3]
The matching function
A matching function is a mathematical relationship that describes the formation of new relationships (also called 'matches') from unmatched agents of the appropriate types. For example, in the context of job formation, matching functions are sometimes assumed to have the following 'Cobb–Douglas' form:
where 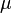 ,
,  , and
, and 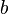 are positive constants.
In this equation,
are positive constants.
In this equation, 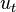 represents the number of unemployed job seekers in the economy at a given time
represents the number of unemployed job seekers in the economy at a given time 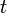 , and
, and 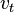 is the number of vacant jobs firms are trying to fill. The number of new relationships (matches) created (per unit of time) is given by
is the number of vacant jobs firms are trying to fill. The number of new relationships (matches) created (per unit of time) is given by 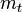 .
.
A matching function is in general analogous to a production function. But whereas a production function usually represents the production of goods and services from inputs like labor and capital, a matching function represents the formation of new relationships from the pools of available unmatched individuals. Estimates of the labor market matching function suggest that it has constant returns to scale, that is, 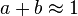 .[4]
.[4]
If the fraction of jobs that separate (due to firing, quits, and so forth) from one period to the next is  ,
then to calculate the change in employment from one period to the next we must add the formation of new matches and subtract off the separation of old matches. A period may be treated as a week, a month, a quarter, or some other convenient period of time, depending on the data under consideration. (For simplicity, we are ignoring the entry of new workers into the labor force, and death or retirement of old workers, but these issues can be accounted for as well.) Suppose we write the number of workers employed in period
,
then to calculate the change in employment from one period to the next we must add the formation of new matches and subtract off the separation of old matches. A period may be treated as a week, a month, a quarter, or some other convenient period of time, depending on the data under consideration. (For simplicity, we are ignoring the entry of new workers into the labor force, and death or retirement of old workers, but these issues can be accounted for as well.) Suppose we write the number of workers employed in period 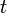 as
as  , where
, where 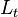 is the labor force in period
is the labor force in period 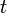 . Then given the matching function described above, the dynamics of employment over time would be given by
. Then given the matching function described above, the dynamics of employment over time would be given by
For simplicity, many studies treat  as a fixed constant. But the fraction of workers separating per period of time can be determined endogenously if we assume that the value of being matched varies over time for each worker-firm pair (due, for example, to changes in productivity).[5]
as a fixed constant. But the fraction of workers separating per period of time can be determined endogenously if we assume that the value of being matched varies over time for each worker-firm pair (due, for example, to changes in productivity).[5]
Applications
Matching theory has been applied in many economic contexts, including:
- Formation of jobs, from unemployed workers and vacancies opened by firms[1][5]
- Formation of marriages, from unmatched individuals
- Allocation of loans from banks to entrepreneurs[6]
- The role of money in facilitating sales when sellers and buyers meet[7]
Controversy
Matching theory has been widely accepted as one of the best available descriptions of the frictions in the labor market, but some economists have recently questioned its quantitative accuracy. While unemployment exhibits large fluctuations over the business cycle, Robert Shimer has demonstrated that standard versions of matching models predict much smaller fluctuations in unemployment.[8]
See also
- Search theory
- Beveridge curve
- Labor economics
- Monetary economics
- Nash bargaining game
- Matching (graph theory)
- Optimal matching
References
- 1 2 Pissarides, Christopher (2000). Equilibrium Unemployment Theory (2nd ed.). MIT Press. ISBN 0-262-16187-7.
- ↑ Economic Prize Committee of the Royal Swedish Academy of Sciences, 'Scientific Background', page 2.
- ↑ http://www.nobelprize.org/nobel_prizes/economics/laureates/2012/
- ↑ Petrongolo, Barbara; Pissarides, Christopher (2001). "Looking into the black box: a survey of the matching function". Journal of Economic Literature 39 (2): 390–431. doi:10.1257/jel.39.2.390. JSTOR 2698244.
- 1 2 Mortensen, Dale; Pissarides, Christopher (1994). "Job creation and job destruction in the theory of unemployment". Review of Economic Studies 61 (3): 397–415. doi:10.2307/2297896.
- ↑ Haan, Wouter den; Ramey, Garey; Watson, Joel (2003). "Liquidity flows and the fragility of business enterprises". Journal of Monetary Economics 50 (6): 1215–1241. doi:10.1016/S0304-3932(03)00077-1.
- ↑ Kiyotaki, Nobuhiro; Wright, Randall (1993). "A search-theoretic approach to monetary economics". American Economic Review 83 (1): 63–77. JSTOR 2117496.
- ↑ Shimer, Robert (2005). "The cyclical behavior of equilibrium unemployment and vacancies". American Economic Review 95 (1): 25–49. doi:10.1257/0002828053828572.
| ||||||||||||||||||||||||||||||