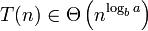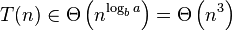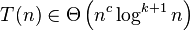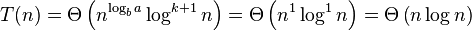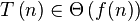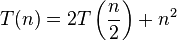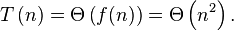Master theorem

For the result in enumerative combinatorics, see MacMahon Master theorem.

For the result about Mellin transforms, see Ramanujan's master theorem.

In the analysis of algorithms, the master theorem provides a solution in asymptotic terms (using Big O notation) for recurrence relations of types that occur in the analysis of many divide and conquer algorithms. It was popularized by the canonical algorithms textbook Introduction to Algorithms by Cormen, Leiserson, Rivest, and Stein, in which it is both introduced and proved. Not all recurrence relations can be solved with the use of the master theorem; its generalizations include the Akra–Bazzi method.

Introduction

Consider a problem that can be solved using a recursive algorithm such as the following:

 procedure T( n : size of problem ) defined as:
   if n < 1 then exit

   Do work of amount f(n)

   repeat for a total of ′a′ times
       T(n/b)
   end repeat
 end procedure

In the above algorithm we are dividing the problem into a number of subproblems recursively, each subproblem being of size $n / b$ . This can be visualized as building a call tree with each node of the tree as an instance of one recursive call and its child nodes being instances of subsequent calls. In the above example, each node would have $a$ number of child nodes. Each node does an amount of work that corresponds to the size of the sub problem $n$ passed to that instance of the recursive call and given by $f(n)$ . The total amount of work done by the entire tree is the sum of the work performed by all the nodes in the tree.

Algorithms such as above can be represented as a recurrence relation 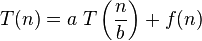$T(n) = a \; T\left(\frac{n}{b}\right) + f(n)$ . This recursive relation can be successively substituted into itself and expanded to obtain expression for total amount of work done.^[1]

The Master theorem allows us to easily calculate the running time of such a recursive algorithm in Θ-notation without doing an expansion of the recursive relation above.

Generic form

The master theorem concerns recurrence relations of the form:

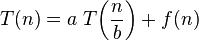T(n) = a \; T\!\left(\frac{n}{b}\right) + f(n)

where

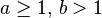
a \geq 1 \mbox{, } b > 1

In the application to the analysis of a recursive algorithm, the constants and function take on the following significance:

n is the size of the problem.
a is the number of subproblems in the recursion.
n/b is the size of each subproblem. (Here it is assumed that all subproblems are essentially the same size.)
f (n) is the cost of the work done outside the recursive calls, which includes the cost of dividing the problem and the cost of merging the solutions to the subproblems.

It is possible to determine an asymptotic tight bound in these three cases:

Case 1

Generic form

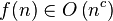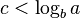If $f(n) \in O\left( n^{c} \right)$ where $c < \log_b a$ (using big O notation)

then:

T(n) \in \Theta\left( n^{\log_b a} \right)

Example

T(n) = 8 T\left(\frac{n}{2}\right) + 1000n^2

As one can see from the formula above:

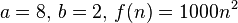a = 8, \, b = 2, \, f(n) = 1000n^2

, so

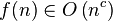f(n) \in O\left(n^c\right)

, where

c = 2

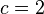
Next, we see if we satisfy the case 1 condition:

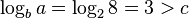\log_b a = \log_2 8 = 3>c

It follows from the first case of the master theorem that

T(n) \in \Theta\left( n^{\log_b a} \right) = \Theta\left( n^{3} \right)

(indeed, the exact solution of the recurrence relation is 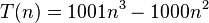$T(n) = 1001 n^3 - 1000 n^2$ , assuming $T(1) = 1$ ).

Case 2

Generic form

If it is true, for some constant k ≥ 0, that:

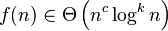f(n) \in \Theta\left( n^{c} \log^{k} n \right)

where

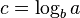
c = \log_b a

then:

T(n) \in \Theta\left( n^{c} \log^{k+1} n \right)

Example

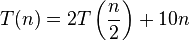
$T(n) = 2 T\left(\frac{n}{2}\right) + 10n$

As we can see in the formula above the variables get the following values:

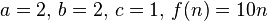
a = 2, \, b = 2, \, c = 1, \, f(n) = 10n

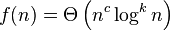f(n) = \Theta\left(n^{c} \log^{k} n\right)

where

c = 1, k = 0

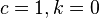
Next, we see if we satisfy the case 2 condition:

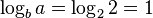\log_b a = \log_2 2 = 1

, and therefore, yes,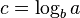

c = \log_b a

So it follows from the second case of the master theorem:

T(n) = \Theta\left( n^{\log_b a} \log^{k+1} n\right) = \Theta\left( n^{1} \log^{1} n\right) = \Theta\left(n \log n\right)

Thus the given recurrence relation T(n) was in Θ(n log n).

(This result is confirmed by the exact solution of the recurrence relation, which is 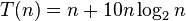$T(n) = n + 10 n\log_2 n$ , assuming $T(1) = 1$ .)

Case 3

Generic form

If it is true that:

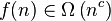f(n) \in \Omega\left( n^{c} \right)

where

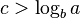
c > \log_b a

and if it is also true that:

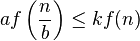a f\left( \frac{n}{b} \right) \le k f(n)

for some constant

k < 1

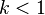and sufficiently large

n

(often called the regularity condition)

then:

T\left(n \right) \in \Theta\left(f(n) \right)

Example

T(n) = 2 T\left(\frac{n}{2}\right) + n^2

As we can see in the formula above the variables get the following values:

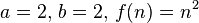
a = 2, \, b = 2, \, f(n) = n^2

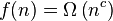f(n) = \Omega\left(n^c\right)

, where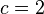

c = 2

Next, we see if we satisfy the case 3 condition:

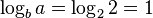\log_b a = \log_2 2 = 1

, and therefore, yes,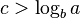

c > \log_b a

The regularity condition also holds:

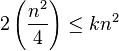2 \left(\frac{n^2}{4}\right) \le k n^2

, choosing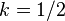

k = 1/2

So it follows from the third case of the master theorem:

T \left(n \right) = \Theta\left(f(n)\right) = \Theta \left(n^2 \right).

Thus the given recurrence relation T(n) was in Θ(n²), that complies with the f (n) of the original formula.

(This result is confirmed by the exact solution of the recurrence relation, which is $T(n) = 2 n^2 - n$ , assuming $T(1) = 1$ .)

Inadmissible equations

The following equations cannot be solved using the master theorem:^[2]

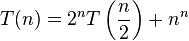
$T(n) = 2^nT\left (\frac{n}{2}\right )+n^n$
a is not a constant; the number of subproblems should be fixed
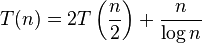
$T(n) = 2T\left (\frac{n}{2}\right )+\frac{n}{\log n}$
non-polynomial difference between f(n) and 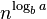$n^{\log_b a}$ (see below)
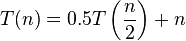
$T(n) = 0.5T\left (\frac{n}{2}\right )+n$
a<1 cannot have less than one sub problem
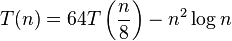
$T(n) = 64T\left (\frac{n}{8}\right )-n^2\log n$
f(n) which is the combination time is not positive
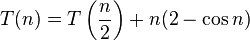
$T(n) = T\left (\frac{n}{2}\right )+n(2-\cos n)$
case 3 but regularity violation.

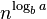In the second inadmissible example above, the difference between $f(n)$ and $n^{\log_b a}$ can be expressed with the ratio 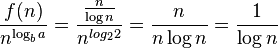$\frac{f(n)}{n^{\log_b a}} = \frac{\frac{n}{\log n}}{n^{log_2 2}} = \frac{n}{n \log n} = \frac{1}{\log n}$ . It is clear that 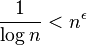$\frac{1}{\log n} < n^\epsilon$ for any constant $\epsilon > 0$ . Therefore, the difference is not polynomial and the Master Theorem does not apply.

Application to common algorithms

Algorithm	Recurrence Relationship	Run time	Comment
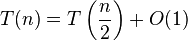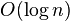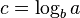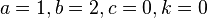Binary search	$T(n) = T\left(\frac{n}{2}\right) + O(1)$	$O(\log n)$	Apply Master theorem case $c = \log_b a$ , where $a = 1, b = 2, c = 0, k = 0$ ^[3]
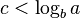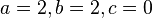Binary tree traversal	$T(n) = 2 T\left(\frac{n}{2}\right) + O(1)$	$O(n)$	Apply Master theorem case $c < \log_b a$ where $a = 2, b = 2, c = 0$ ^[3]
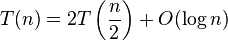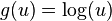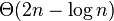Optimal Sorted Matrix Search	$T(n) = 2 T\left(\frac{n}{2}\right) + O(\log n)$	$O(n)$	Apply the Akra–Bazzi theorem for $p=1$ and $g(u)=\log(u)$ to get $\Theta(2n - \log n)$
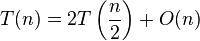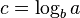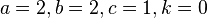Merge Sort	$T(n) = 2 T\left(\frac{n}{2}\right) + O(n)$	$O(n \log n)$	Apply Master theorem case $c = \log_b a$ , where $a = 2, b = 2, c = 1, k = 0$

Notes

↑ Duke University, "Big-Oh for Recursive Functions: Recurrence Relations", http://www.cs.duke.edu/~ola/ap/recurrence.html
↑ Massachusetts Institute of Technology (MIT), "Master Theorem: Practice Problems and Solutions", http://www.csail.mit.edu/~thies/6.046-web/master.pdf
1 2 Dartmouth College, http://www.math.dartmouth.edu/archive/m19w03/public_html/Section5-2.pdf

References

Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw–Hill, 2001. ISBN 0-262-03293-7. Sections 4.3 (The master method) and 4.4 (Proof of the master theorem), pp. 73–90.
Michael T. Goodrich and Roberto Tamassia. Algorithm Design: Foundation, Analysis, and Internet Examples. Wiley, 2002. ISBN 0-471-38365-1. The master theorem (including the version of Case 2 included here, which is stronger than the one from CLRS) is on pp. 268–270.

This article is issued from Wikipedia - version of the Monday, February 15, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Master theorem

Introduction

Generic form

Case 1

Generic form

Example

Case 2

Generic form

Example

Case 3

Generic form

Example

Inadmissible equations

See also

Application to common algorithms

Notes

References