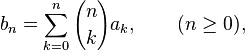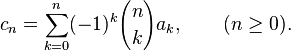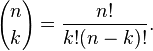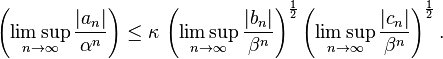Mashreghi–Ransford inequality
In Mathematics, the Mashreghi–Ransford inequality is a bound on the growth rate of certain sequences. It is named after J. Mashreghi and T. Ransford.
Let 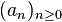 be a sequence of complex numbers, and let
be a sequence of complex numbers, and let
and
We remind that the binomial coefficients are defined by
Assume that, for some 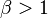 , we have
, we have 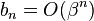 and
and 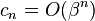 as
as 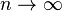 . Then
. Then
-
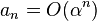 , as
, as 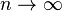 ,
,
where 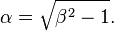
Moreover, there is a universal constant 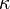 such that
such that
The precise value of 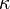 is unknown. However, it is known that
is unknown. However, it is known that
References
- Mashreghi, J.; Ransford, T. (2005). "Binomial sums and functions of exponential type". B. London Math. Soc. 37 (01): 15–24..
This article is issued from Wikipedia - version of the Tuesday, April 07, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.