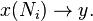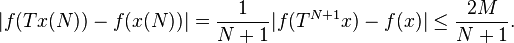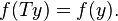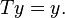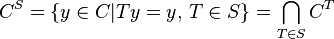Markov–Kakutani fixed-point theorem

In mathematics, the Markov–Kakutani fixed-point theorem, named after Andrey Markov and Shizuo Kakutani, states that a commuting family of continuous affine self-mappings of a compact convex subset in a locally convex topological vector space has a common fixed point.

Statement

Let E be a locally convex topological vector space. Let C be a compact convex subset of E. Let S be a commuting family of self-mappings T of C which are continuous and affine, i.e. T(tx +(1 – t)y) = tT(x) + (1 – t)T(y) for t in [0,1] and x, y in C. Then the mappings have a common fixed point in C.

Proof for a single affine self-mapping

Let T be a continuous affine self-mapping of C.

For x in C define other elements of C by

x(N)={1\over N+1}\sum_{n=0}^N T^n(x).

Since C is compact, there is a convergent subnet in C:

x(N_i)\rightarrow y. \,

To prove that y is a fixed point, it suffices to show that f(Ty) = f(y) for every f in the dual of E. Since C is compact, |f| is bounded on C by a positive constant M. On the other hand

|f(Tx(N))-f(x(N))|={1\over N+1} |f(T^{N+1}x)-f(x)|\le {2M\over N+1}.

Taking N = N_i and passing to the limit as i goes to infinity, it follows that

f(Ty) = f(y). \,

Hence

Ty = y. \,

Proof of theorem

The set of fixed points of a single affine mapping T is a non-empty compact convex set C^T by the result for a single mapping. The other mappings in the family S commute with T so leave C^T invariant. Applying the result for a single mapping successively, it follows that any finite subset of S has a non-empty fixed point set given as the intersection of the compact convex sets C^T as T ranges over the subset. From the compactness of C it follows that the set

C^S=\{y\in C|Ty=y, \, T\in S\}=\bigcap_{T\in S} C^T \,

is non-empty (and compact and convex).

References

Markov, A. (1936), "Quelques théorèmes sur les ensembles abéliens", Dokl. Akad. Nauk. SSSR 10: 311–314
Kakutani, S. (1938), "Two fixed point theorems concerning bicompact convex sets", Proc. Imp. Akad. Tokyo 14: 242–245
Reed, M.; Simon, B. (1980), Functional Analysis, Methods of Mathematical Physics 1 (2nd revised ed.), Academic Press, p. 152, ISBN 0-12-585050-6

This article is issued from Wikipedia - version of the Monday, July 06, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.