Marcus theory
Marcus theory is a theory originally developed by Rudolph A. Marcus, starting in 1956, to explain the rates of electron transfer reactions – the rate at which an electron can move or jump from one chemical species (called the electron donor) to another (called the electron acceptor).[1] It was originally formulated to address outer sphere electron transfer reactions, in which the two chemical species only change in their charge with an electron jumping (e.g. the oxidation of an ion like Fe2+/Fe3+), but do not undergo large structural changes. It was extended to include inner sphere electron transfer contributions, in which a change of distances or geometry in the solvation or coordination shells of the two chemical species is taken into account (the Fe-O distances in Fe(H2O)2+ and Fe(H2O)3+ are different).[2][3]
For electron transfer reactions without making or breaking bonds Marcus theory takes the place of Eyring's transition state theory [4][5] which has been derived for reactions with structural changes. Both theories lead to rate equations of the same exponential form. However, whereas in Eyring theory the reaction partners become strongly coupled in the course of the reaction to form a structurally defined activated complex, in Marcus theory they are weakly coupled and retain their individuality. It is the thermally induced reorganization of the surroundings, the solvent (outer sphere) and the solvent sheath or the ligands (inner sphere) which create the geometrically favourable situation prior to and independent of the electron jump.
The original classical Marcus theory for outer sphere electron transfer reactions demonstrates the importance of the solvent and leads the way to the calculation of the Gibbs free energy of activation, using the polarization properties of the solvent, the size of the reactants, the transfer distance and the Gibbs free energy  G0 of the redox reaction. The most startling result of Marcus' theory was the "inverted region": whereas the reaction rates usually become higher with increasing exergonicity of the reaction, electron transfer should, according to Marcus theory, become slower in the very negative
G0 of the redox reaction. The most startling result of Marcus' theory was the "inverted region": whereas the reaction rates usually become higher with increasing exergonicity of the reaction, electron transfer should, according to Marcus theory, become slower in the very negative  G0 domain. Scientists searched the inverted region for proof of a slower electron transfer rate for 30 years until it was unequivocally verified experimentally in 1984.
G0 domain. Scientists searched the inverted region for proof of a slower electron transfer rate for 30 years until it was unequivocally verified experimentally in 1984.
R.A. Marcus received the Nobel Prize in Chemistry in 1992 for this theory. Marcus theory is used to describe a number of important processes in chemistry and biology, including photosynthesis, corrosion, certain types of chemiluminescence, charge separation in some types of solar cell and more. Besides the inner and outer sphere applications, Marcus theory has been extended to address heterogeneous electron transfer.
The one-electron redox reaction
Chemical reactions may lead to a substitution of a group in a molecule or a ligand in a complex, to the elimination of a group of the molecule or a ligand, or to a rearrangement of a molecule or complex. An electron-transfer reaction may, however, also cause simply an exchange of charges between the reactants, and these redox reactions without making or breaking a bond seem to be quite simple in inorganic chemistry for ions and complexes. These reactions often become manifest by a change of colour, e.g. for ions or complexes of transition metal ions, but organic molecules, too, may change their colour by accepting or giving away an electron (like the herbicide Paraquat (N,N-dimethyl-4,4'-bipyridinium dichloride) which becomes blue when accepting an electron, thence the alternative name of methyl viologen). For this type of electron-transfer reactions R.A. Marcus has developed his theory. Here the trace of argument and the results are presented. For the mathematical development and details the original papers[6][7] should be consulted.
In a redox reaction one partner acts as an electron donor D the other as an acceptor A. For a reaction to take place D and A must diffuse together. They form the precursor complex, usually a kinetic, unstable, solvated encounter complex, which by electron transfer is transformed to the successor complex, and finally this separates by diffusion. For a one electron transfer the reaction is
(D and A may already carry charges). Here k12, k21 and k30 are diffusion constants, k23 and k32 rate constants of activated reactions. The total reaction may be diffusion controlled (the electron transfer step is faster than diffusion, every encounter leads to reaction) or activation controlled (the "equilibrium of association" is reached, the electron transfer step is slow, the separation of the successor complex is fast).
Outer sphere electron transfer
Redox reactions are preferably run in polar solvents. Donor and acceptor then have a solvent shell and the precursor and successor complexes are solvated also. The closest molecules of the solvent shell, or the ligands in complexes, are tightly bound and constitute the "inner sphere". Reactions in which these participate are called inner sphere redox reactions. The free solvent molecules constitute the "outer sphere". Outer sphere redox reactions do not change the inner sphere, no bonds are made nor broken.
It was R.A. Marcus who realized the role of the solvent when he worked on the nature and magnitude of the Gibbs free energy of activation for redox reactions, more precisely: one-electron transfer reactions of the outer sphere type. He published two fundamental papers.[6][7] The ideas of these two papers are often referred to Marcus Theory although Marcus’ later work goes much beyond them.[1] In the following the development and results of the ideas of these two papers are outlined. For the mathematics and more details the original papers should be consulted.
The problem
In outer sphere redox reactions no bonds are formed or broken; only an electron transfer (ET) takes place. A quite simple example is the Fe2+/Fe3+ redox reaction, the self exchange reaction which is known to be always occurring in an aqueous solution containing both FeSO4 and Fe2(SO4)3 (of course, with equal and measurable rates in both directions and with Gibbs free reaction energy  G0 = 0).
G0 = 0).
From the reaction rate's temperature dependence an activation energy is determined, and this activation energy is interpreted as the energy of the transition state in a reaction diagram. The latter is drawn, according to Arrhenius and Eyring, as an energy diagram with the reaction coordinate as the abscissa. The reaction coordinate describes the minimum energy path from the reactants to the products, and the points of this coordinate are combinations of distances and angles between and in the reactants in the course of the formation and/or cleavage of bonds. The maximum of the energy diagram, the transition state, is characterized by a specific configuration of the atoms. Moreover, in Eyring's TST [4][5] a quite specific change of the nuclear coordinates is responsible for crossing the maximum point, a vibration in this direction is consequently treated as a translation.
For outer sphere redox reactions there cannot be such a reaction path, but nevertheless one does observe an activation energy. The rate equation for activation-controlled reactions has the same exponential form as the Eyring equation,
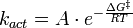
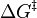 is the Gibbs free energy of the formation of the transition state, the exponential term represents the probability of its formation, A contains the probability of crossing from precursor to successor complex.
is the Gibbs free energy of the formation of the transition state, the exponential term represents the probability of its formation, A contains the probability of crossing from precursor to successor complex.
The Marcus model
The consequence of an electron transfer is the rearrangement of charges, and this gravely influences the solvent environment. For the dipolar solvent molecules rearrange in the direction of the field of the charges (this is called orientation polarisation), and also the atoms and electrons in the solvent molecules are slightly displaced (atomic and electron polarization, respectively). It is this solvent polarization which determines the free energy of activation and thus the reaction rate.
Substitution, elimination and isomerization reactions differ from the outer sphere redox reaction not only in the structural changes outlined above, but also in the fact that the movements of the nuclei and the shift of charges (charge transfer, CT) on the reactions path take place in a continuous and concerted way: nuclear configurations and charge distribution are always "in equilibrium". This is illustrated by the SN2 substitution of the saponification of an alkyl halide where the rear side attack of the OH− ion pushes out a halide ion and where a transition state with a five-coordinated carbon atom must be visualized. The system of the reactants becomes coupled so tightly during the reaction that they form the activated complex as an integral entity. The solvent here has a minor effect.
By contrast, in outer sphere redox reactions the displacement of nuclei in the reactants are small, here the solvent has the dominant role. Donor-acceptor coupling is weak, both keep their identity during the reaction. Therefore, the electron, being an elementary particle, can only "jump" as a whole (electron transfer, ET). If the electron jumps, the transfer is much faster than the movement of the large solvent molecules, with the consequence that the nuclear positions of the reaction partners and the solvent molecules are the same before and after the electron jump (Franck–Condon principle).[8] The jump of the electron is governed by quantum mechanical rules, it is only possible if also the energy of the ET system does not change "during" the jump.
The arrangement of solvent molecules depends on the charge distribution on the reactants. If the solvent configuration must be the same before and after the jump and the energy may not change, then the solvent cannot be in the solvation state of the precursor nor in that of the successor complex as they are different, it has to be somewhere in between. For the self-exchange reaction for symmetry reasons an arrangement of the solvent molecules exactly in the middle of those of precursor and successor complex would meet the conditions. This means that the solvent arrangement with half of the electron on both donor and acceptor would be the correct environment for jumping. Also, in this state the energy of precursor and successor in their solvent environment would be the same.
However, the electron as an elementary particle cannot be divided, it resides either on the donor or the acceptor and arranges the solvent molecules accordingly in an equilibrium. The "transition state", on the other hand, requires a solvent configuration which would result from the transfer of half an electron, which is impossible. This means that real charge distribution and required solvent polarization are not in an "equilibrium". Yet it is possible that the solvent takes a configuration corresponding to the "transition state", even if the electron sits on the donor or acceptor. This, however, requires energy. This energy may be provided by the thermal energy of the solvent and thermal fluctuations can produce the correct polarization state. Once this has been reached the electron can jump. The creation of the correct solvent arrangement and the electron jump are decoupled and do not happen in a synchronous process. Thus the energy of the transition state is mostly polarization energy of the solvent.
Marcus theory
The macroscopic system: two conducting spheres
On the basis of his reasoning R.A. Marcus developed a classical theory with the aim of calculating the polarization energy of the said non-equilibrium state. From thermodynamics it is well known that the energy of such a state can be determined if a reversible path to that state is found. Marcus was successful finding such a path via two reversible charging steps for the preparation of the "transition state" from the precursor complex.
Four elements are essential for the model on which the theory is based: (1) Marcus employs a classical, purely electrostatic model. The charge (many elementary charges) may be transferred in any portion from one body to another. (2) Marcus separates the fast electron polarisation Pe and the slow atom and orientation polarisation Pu of the solvent on grounds of their time constants differing several orders of magnitude. (3) Marcus separates the inner sphere (reactant + tightly bound solvent molecules, in complexes + ligands) and the outer sphere (free solvent ) (4) In this model Marcus confines himself to calculating the outer sphere energy of the non-equilibrium polarization of the "transition state". The outer sphere energy is often much larger than the inner sphere contribution because of the far reaching electrostatic forces (compare the Debye-Hückel theory of electrochemistry).
Marcus’ tool is the theory of dielectric polarization in solvents. He solved the problem in a general way for a transfer of charge between two bodies of arbitrary shape with arbitrary surface and volume charge. For the self-exchange reaction, the redox pair (e.g. Fe(H2O)63+ / Fe(H2O)62+) is substituted by two macroscopic conducting spheres at a defined distance carrying specified charges. Between these spheres a certain amount of charge is reversibly exchanged.
In the first step the energy WI of the transfer of a specific amount of charge is calculated, e.g. for the system in a state when both spheres carry half of the amount of charge which is to be transferred. This state of the system can be reached by transferring the respective charge from the donor sphere to the vacuum and then back to the acceptor sphere.[9] Then the spheres in this state of charge give rise to a defined electric field in the solvent which creates the total solvent polarization Pu + Pe. By the same token this polarization of the solvent interacts with the charges.
In a second step the energy WII of the reversible (back) transfer of the charge to the first sphere, again via the vacuum, is calculated. However, the atom and orientation polarization Pu is kept fixed, only the electron polarization Pe may adjust to the field of the new charge distribution and the fixed Pu. After this second step the system is in the desired state with an electron polarization corresponding to the starting point of the redox reaction and an atom and orientation polarization corresponding to the "transition state". The energy WI + WII of this state is, thermodynamically speaking, a Gibbs free energy G.

 e or the induced polarization P, the ordinate the Gibbs free energy. ΔG(0)‡ = λo/4 is the reorganization energy at Δe = 0.5, it corresponds to the activation energy of the self-exchange reaction.
e or the induced polarization P, the ordinate the Gibbs free energy. ΔG(0)‡ = λo/4 is the reorganization energy at Δe = 0.5, it corresponds to the activation energy of the self-exchange reaction.Of course, in this classical model the transfer of any arbitrary amount of charge  e is possible. So the energy of the non-equilibrium state, and consequently of the polarization energy of the solvent, can be probed as a function of
e is possible. So the energy of the non-equilibrium state, and consequently of the polarization energy of the solvent, can be probed as a function of  e. Thus Marcus has lumped together, in a very elegant way, the coordinates of all solvent molecules into a single coordinate of solvent polarization
e. Thus Marcus has lumped together, in a very elegant way, the coordinates of all solvent molecules into a single coordinate of solvent polarization  p which is determined by the amount of transferred charge
p which is determined by the amount of transferred charge  e. So he reached a simplification of the energy representation to only two dimensions: G = f(
e. So he reached a simplification of the energy representation to only two dimensions: G = f( e). The result for two conducting spheres in a solvent is the formula of Marcus
e). The result for two conducting spheres in a solvent is the formula of Marcus
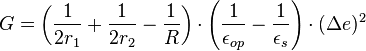
Where r1 and r2 are the radii of the spheres and R is their separation,  s and
s and  op are the static and high frequency (optical) dielectric constants of the solvent,
op are the static and high frequency (optical) dielectric constants of the solvent,  e the amount of charge transferred. The graph of G vs.
e the amount of charge transferred. The graph of G vs.  e is a parabola (Fig. 1). In Marcus theory the energy belonging to the transfer of a unit charge (
e is a parabola (Fig. 1). In Marcus theory the energy belonging to the transfer of a unit charge ( e = 1) is called the (outer sphere) reorganization energy
e = 1) is called the (outer sphere) reorganization energy  o, i.e. the energy of a state where the polarization would correspond to the transfer of a unit amount of charge, but the real charge distribution is that before the transfer.[10] In terms of exchange direction the system is symmetric.
o, i.e. the energy of a state where the polarization would correspond to the transfer of a unit amount of charge, but the real charge distribution is that before the transfer.[10] In terms of exchange direction the system is symmetric.
The microscopic system: the donor-acceptor pair
Shrinking the two-sphere model to the molecular level creates the problem that in the self-exchange reaction the charge can no longer be transferred in arbitrary amounts, but only as a single electron. However, the polarization still is determined by the total ensemble of the solvent molecules and therefore can still be treated classically, i.e. the polarization energy is not subject to quantum limitations. Therefore, the energy of solvent reorganization can be calculated as being due to a hypothetical transfer and back transfer of a partial elementary charge according to the Marcus formula. Thus the reorganization energy for chemical redox reactions, which is a Gibbs free energy, is also a parabolic function of  e of this hypothetical transfer, For the self exchange reaction, where for symmetry reasons
e of this hypothetical transfer, For the self exchange reaction, where for symmetry reasons  e = 0.5, the Gibbs free energy of activation is
e = 0.5, the Gibbs free energy of activation is  G(0)‡ =
G(0)‡ =  o/4 (see Fig. 1 and Fig. 2 intersection of the parabolas I and f, f(0), respectively).
o/4 (see Fig. 1 and Fig. 2 intersection of the parabolas I and f, f(0), respectively).
Up to now all was physics, now some chemistry enters. The self exchange reaction is a very specific redox reaction, most of the redox reactions are between different partners [11] e.g.
and they have positive (endergonic) or negative (exergonic) Gibbs free energies of reaction  G0.
G0.
As Marcus calculations refer exclusively to the electrostatic properties in the solvent (outer sphere)  G0 and
G0 and  o are independent of one another and therefore can just be added up. This means that the Marcus parabolas in systems with different
o are independent of one another and therefore can just be added up. This means that the Marcus parabolas in systems with different  G0 are shifted just up or down in the G vs.
G0 are shifted just up or down in the G vs.  e diagram (Fig. 2). Variation of
e diagram (Fig. 2). Variation of  G0 can be affected in experiments by offering different acceptors to the same donor.
G0 can be affected in experiments by offering different acceptors to the same donor.
Simple calculations of the points of intersection of the parabolas i ( ),
), 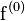 (
(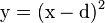 ) and
) and 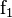 to
to 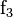 (
(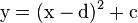 ) give the Gibbs free energy of activation
) give the Gibbs free energy of activation
It should be noted that the intersection of those parabolas represents an activation energy and not the energy of a transition state of fixed configuration of all nuclei in the system as is the case in the substitution and other reactions mentioned. The transition state of the latter reactions has to meet structural and energetic conditions, redox reactions have only to comply to the energy requirement. Whereas the geometry of the transition state in the other reactions is the same for all pairs of reactants, for redox pairs many polarization environments may meet the energetic conditions.

Marcus’ formula shows a quadratic dependence of the Gibbs free energy of activation on the Gibbs free energy of reaction. It is general knowledge from the host of chemical experience that reactions usually are the faster the more negative is  G0. In many cases even a linear free energy relation is found. According to the Marcus formula the rates increase also when the reactions are more exergonic, however only as long as
G0. In many cases even a linear free energy relation is found. According to the Marcus formula the rates increase also when the reactions are more exergonic, however only as long as  G0 is positive or slightly negative. It is surprising that for redox reactions according to the Marcus formula the activation energy should increase for very exergonic reaction, i.e. in the cases when
G0 is positive or slightly negative. It is surprising that for redox reactions according to the Marcus formula the activation energy should increase for very exergonic reaction, i.e. in the cases when  G0 is negative and its absolute value is greater than that of
G0 is negative and its absolute value is greater than that of  o. This realm of Gibbs free energy of reaction is called "Marcus inverted region". In Fig. 2 it becomes obvious that the intersection of the parabolas i and f moves upwards in the left part of the graph when
o. This realm of Gibbs free energy of reaction is called "Marcus inverted region". In Fig. 2 it becomes obvious that the intersection of the parabolas i and f moves upwards in the left part of the graph when  G0 continues to become more negative, and this means increasing activation energy. Thus the total graph of ln k vs.
G0 continues to become more negative, and this means increasing activation energy. Thus the total graph of ln k vs.  G0 should have a maximum.
G0 should have a maximum.
The maximum of the ET rate is expected at  G‡ = 0. Here
G‡ = 0. Here  e = 0 and q = 0 (Fig. 2) which means that the electron may jump in the precursor complex at its equilibrium polarization. No thermal activation is necessary: the reaction is barrierless. In the inverted region the polarization corresponds to the difficult to imagine notion of a charge distribution where the donor has received and the acceptor given off charge. Of course, in real world this does not happen, it is not a real charge distribution which creates this critical polarization, but the thermal fluctuation in the solvent. This polarization necessary for transfer in the inverted region can be created – with some probability – as well as any other one.[12] The electron is just waiting for it for jumping.
e = 0 and q = 0 (Fig. 2) which means that the electron may jump in the precursor complex at its equilibrium polarization. No thermal activation is necessary: the reaction is barrierless. In the inverted region the polarization corresponds to the difficult to imagine notion of a charge distribution where the donor has received and the acceptor given off charge. Of course, in real world this does not happen, it is not a real charge distribution which creates this critical polarization, but the thermal fluctuation in the solvent. This polarization necessary for transfer in the inverted region can be created – with some probability – as well as any other one.[12] The electron is just waiting for it for jumping.
Inner sphere electron transfer
In the outer sphere model the donor or acceptor and the tightly bound solvation shells or the complex’ ligands were considered to form rigid structures which do not change in the course of electron transfer. However, the distances in the inner sphere are dependent on the charge of donor and acceptor, e.g. the central ion-ligand distances are different in complexes carrying different charges And again the Franck–Condon principle must be obeyed: for the electron to jump to occur, the nuclei have to have a configuration which is an identical one of as well the precursor as the successor complexes, of course highly distorted. In this case the energy requirement is fulfilled automatically.
In this inner sphere case the Arrhenius concept holds, the transition state of definite geometric structure is reached along a geometrical reaction coordinate determined by nuclear motions. No further nuclear motion is necessary to form the successor complex, just the electron jumps, which makes a difference to the TST theory. The reaction coordinate for inner sphere energy is governed by vibrations and they differ in the oxidized and reduces species.[13]
For the self-exchange system Fe2+/Fe3+ only the symmetrical breathing vibration of the six water molecules around the iron ions is considered.[13] Assuming harmonic conditions this vibration has frequencies 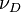 and
and 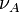 , the force constants fD and fA are
, the force constants fD and fA are 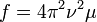 and the energies are
and the energies are
where q0 is the equilibrium normal coordinate and 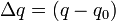 the displacement along the normal coordinate, the factor 3 stems from 6 (H2O)
the displacement along the normal coordinate, the factor 3 stems from 6 (H2O) ½. Like for the outer-sphere reorganization energy potential energy curve is quadratic, here, however, as a consequence of vibrations.
½. Like for the outer-sphere reorganization energy potential energy curve is quadratic, here, however, as a consequence of vibrations.
The equilibrium normal coordinates differ in Fe(H2O)62+ and Fe(H2O)63+. By thermal excitation of the breathing vibration a geometry can be reached which is common to both donor and acceptor, i.e. the potential energy curves of the breathing vibrations of D and A intersect here. This is the situation where the electron may jump. The energy of this transition state is the inner sphere reorganization energy  in.
in.
For the self-exchange reaction the metal-water distance in the transition state can be calculated [13]
This gives the inner sphere reorganisation energy
It is fortunate that the expressions for the energies for outer and inner reorganization have the same quadratic form. Inner sphere and outer sphere reorganization energies are independent, so they can be added to give 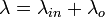 and inserted in the Arrhenius equation
and inserted in the Arrhenius equation
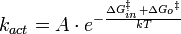
Here, A can be seen to represent the probability of electron jump, exp[- Gin
Gin /kT] that of reaching the transition state of the inner sphere and exp[-
/kT] that of reaching the transition state of the inner sphere and exp[- Go
Go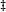 /kT] that of outer sphere adjustment .
For unsymmetrical (cross) reactions like
/kT] that of outer sphere adjustment .
For unsymmetrical (cross) reactions like
the expression for 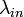 can also be derived, but it is more complicated.[13] These reactions have a free reaction enthalpy
can also be derived, but it is more complicated.[13] These reactions have a free reaction enthalpy  G0 which is independent of the reorganization energy and determined by the different redox potentials of the iron and cobalt couple. Consequently, the quadratic Marcus equation holds also for the inner sphere reorganization energy, including the prediction of an inverted region. One may visualizing this by (a) in the normal region both the initial state and the final state have to have stretched bonds, (b) In the
G0 which is independent of the reorganization energy and determined by the different redox potentials of the iron and cobalt couple. Consequently, the quadratic Marcus equation holds also for the inner sphere reorganization energy, including the prediction of an inverted region. One may visualizing this by (a) in the normal region both the initial state and the final state have to have stretched bonds, (b) In the  G
G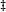 = 0 case the equilibrium configuration of the initial state is the stretched configuration of the final state, and (c) in the inverted region the initial state has compressed bonds whereas the final state has largely stretched bonds.
Similar considerations hold for metal complexes where the ligands are larger than solvent molecules and also for ligand bridged polynuclear complexes.
= 0 case the equilibrium configuration of the initial state is the stretched configuration of the final state, and (c) in the inverted region the initial state has compressed bonds whereas the final state has largely stretched bonds.
Similar considerations hold for metal complexes where the ligands are larger than solvent molecules and also for ligand bridged polynuclear complexes.
The probability of the electron jump
The strength of the electronic coupling of the donor and acceptor decides whether the electron transfer reaction is adiabatic or non-adiabatic. In the non-adiabatic case the coupling is weak, i.e. HAB in Fig. 3 is small compared to the reorganization energy and donor and acceptor retain their identity. The system has a certain probability to jump from the initial to the final potential energy curves. In the adiabatic case the coupling is considerable, the gap of 2 HAB is larger and the system stays on the lower potential energy curve.[14]
Marcus theory as laid out above, represents the non-adiabatic case.[15] Consequently, the semi-classical Landau-Zener theory can be applied, which gives the probability of interconversion of donor and acceptor for a single passage of the system through the region of the intersection of the potential energy curves
where Hif is the interaction energy at the intersection, v the velocity of the system through the intersection region, si and sf the slopes there.
Fig. 3 Energy diagram for Electron Transfer including inner and outer sphere reorganization and electronic coupling: The vertical axis is the free energy, and the horizontal axis is the "reaction coordinate" – a simplified axis representing the motion of all the atomic nuclei (inclusive solvent reorganization)
Working this out, one arrives at the basic equation of Marcus theory
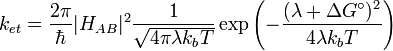
where 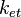 is the rate constant for electron transfer,
is the rate constant for electron transfer, 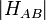 is the electronic coupling between the initial and final states,
is the electronic coupling between the initial and final states,  is the reorganization energy (both inner and outer-sphere), and
is the reorganization energy (both inner and outer-sphere), and 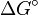 is the total Gibbs free energy change for the electron transfer reaction (
is the total Gibbs free energy change for the electron transfer reaction (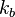 is the Boltzmann constant and
is the Boltzmann constant and  is the absolute temperature).
is the absolute temperature).
Thus Marcus's theory builds on the traditional Arrhenius equation for the rates of chemical reactions in two ways: 1. It provides a formula for the activation energy, based on a parameter called the reorganization energy, as well as the Gibbs free energy. The reorganization energy is defined as the energy required to "reorganize" the system structure from initial to final coordinates, without making the charge transfer. 2. It provides a formula for the pre-exponential factor in the Arrhenius equation, based on the electronic coupling between the initial and final state of the electron transfer reaction (i.e., the overlap of the electronic wave functions of the two states).
Experimental results
Marcus published his theory in 1956. For long years there was an intensive search for the inverted region which would be a proof of the theory. But all experiments with series of reactions of more and more negative  G0 revealed only an increase of the reaction rate up to the diffusion limit, i.e. to a value indicating that every encounter lead to electron transfer, and that limit held also for very negative
G0 revealed only an increase of the reaction rate up to the diffusion limit, i.e. to a value indicating that every encounter lead to electron transfer, and that limit held also for very negative  G0 values (Rehm-Weller behaviour).[16] It took about 30 years until the inverted region was unequivocally substantiated by Miller, Calcaterra and Closs for an intermolecular electron transfer in a molecule where donor and acceptor are kept at a constant distance by means of a stiff spacer (Fig.4).[17]
G0 values (Rehm-Weller behaviour).[16] It took about 30 years until the inverted region was unequivocally substantiated by Miller, Calcaterra and Closs for an intermolecular electron transfer in a molecule where donor and acceptor are kept at a constant distance by means of a stiff spacer (Fig.4).[17]

A posteriori one may presume that in the systems where the reaction partners may diffuse freely the optimum distance for the electron jump may be sought, i.e. the distance for which  G‡ = 0 and
G‡ = 0 and  G0 = -
G0 = -  o. For
o. For  o is dependent on R,
o is dependent on R,  o increases for larger R and the opening of the parabola smaller. It is formally always possible to close the parabola in Fig. 2 to such an extent, that the f-parabola intersects the i-parabola in the apex. Then always
o increases for larger R and the opening of the parabola smaller. It is formally always possible to close the parabola in Fig. 2 to such an extent, that the f-parabola intersects the i-parabola in the apex. Then always  G‡ = 0 and the rate k reaches the maximum diffusional value for all very negative
G‡ = 0 and the rate k reaches the maximum diffusional value for all very negative  G0. There are, however, other concepts for the phenomenon,[1] e.g. the participation of excited states or that the decrease of the rate constants would be so far in the inverted region that it escapes measurement.
G0. There are, however, other concepts for the phenomenon,[1] e.g. the participation of excited states or that the decrease of the rate constants would be so far in the inverted region that it escapes measurement.
R. A. Marcus and his coworkers have further developed the theory outlined here in several aspects. They have included inter alia statistical aspects and quantum effects,[19] they have applied the theory to chemiluminescence [20] and electrode reactions.[21] R. A. Marcus received the Nobel Prize in Chemistry in 1992, and his Nobel Lecture gives an extensive view of his work.[1]
See also
References
- 1 2 3 4 "Electron Transfer Reactions in Chemistry: Theory and Experiment" (PDF). Nobelstiftung (in German). Retrieved 02.04.2007. Check date values in:
|access-date=(help) - ↑ Contrary to Marcus' approach the inner sphere electron transfer theory of Noel S. Hush refers to a continuous change of the electron density during transfer along a geometrical coordinate (adiabatic case), and takes also into account the solvent influence as did Marcus. Hush's formulation is known as Marcus-Hush theory.
- ↑ Hush, N.S. Trans. Faraday Soc. 1961, 57,557
- 1 2 P. W. Atkins: Physical Chemistry, 6. Ed., Oxford University Press, Oxford 1998 p.830
- 1 2 R.S. Berry, S. A. Rice, J. Ross: Physical Chemistry, Wiley, New York 1980, S. 1147 ff,
- 1 2 Marcus, R.A. "On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer I" J.Chem.Phys.1956, 24, 966. doi:10.1063/1.1742723 or Free Text
- 1 2 Marcus.R.A. "Electrostatic Free Energy and Other Properties of States Having Nonequilibrium Polarization I. J.Chem.Phys.1956, 24, 979. doi:10.1063/1.1742724 or Free Text
- ↑ W.F. Libby, "Theory of Electron Exchange Reactions in Aquous Solution" J.Phys.Chem. 1952, 56, 863
- ↑ Marcus takes the vacuum state of the reactants as the zero energy point. Therefore many of his equations contain also the solvation energy of the isolated species Wiso and the electrostatic energy of formation of the precursor and successor complexes.
- ↑ Note: The quadratic dependence of outer sphere reorganization energy is not a consequence of vibrations in reactants or solvent!
- ↑ they are often called Marcus cross reactions.
- ↑ The reverse reaction may support understanding: for this reaction the polarization due to the hypothetical transfer of a unit electron charge is not sufficient to reach a polarization where the polarization energies of A/D and A−/D+ are equal. This can only happen on the hypothetical transfer of more that one electron charge.
- 1 2 3 4 N. Sutin, 'Theory of Electron Transfer Reactions: Insights and Hindsights', Progr. Inorg. Chem. 1083, 30, 441-448
- ↑ In normal chemical reactions, like substitutions, which proceed via a transition state the upper potential energy curve is so far up that it is neglected
- ↑ The theory of adiabatic electron transfer with participation of nuclear movement (which may be considered as a transfer of charge, not an electron jump), has been worked out by Hush.
- ↑ Rehm, D., Weller, A. "Kinetik und Mechanismus der Elektronenübertragung bei der Fluoreszenzlöschung in Acetonitril" Ber. Bunsenges.Physik.Chem. 1969, 73, 834-839 characterized this behaviour by the empirical formula
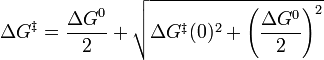
- ↑ Miller J.R., Calcaterra L.T., Closs G.L.: "Intramolecular long-distance electron transfer in radical anions. The effects of free energy and solvent on the reaction rates", J.Am.Chem.Soc. 1984, 106, 3047, doi:10.1021/ja00322a058
- ↑ We recommend reference to the original paper, JACS does not license Wikipedia for graphs.
- ↑ Siders, P.,Marcus, R. A. "Quantum Effects in Electron-Transfer Reactions" J.Am.Chem.Soc. 1981,103,741; Siders, P., Marcus, R. A. "Quantum Effects for Electron-Transfer Reactions in the 'Inverted Region'" J.Am.Chem.Soc. 1981,103,748
- ↑ Marcus. R.A. "On the Theory of Chemiluminescent Electron-Transfer Reactions" J.Chem.Phys. 1965,43,2654
- ↑ Marcus, R. A. "On the theory of Electron-Transfer Reaction IV. Unified Treatment of Homogeneous and Electrode Reactions" J.Chem.Phys. 1965, 43. 679
Marcus's key papers
- Marcus, R.A (1956). "On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. I". J. Chem. Phys. 24 (5): 966. Bibcode:1956JChPh..24..966M. doi:10.1063/1.1742723.
- Marcus, R.A (1956). "Electrostatic Free Energy and Other Properties of States Having Nonequilibrium Polarization. I". J. Chem. Phys. 24 (5): 979. Bibcode:1956JChPh..24..979M. doi:10.1063/1.1742724.
- Marcus, R.A (1957). "On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. II. Applications to Data on the Rates of Isotopic Exchange Reactions". J. Chem. Phys. 26 (4): 867. Bibcode:1957JChPh..26..867M. doi:10.1063/1.1743423.
- Marcus, R.A (1957). "On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. III. Applications to Data on the Rates of Organic Redox Reactions". J. Chem. Phys. 26 (4): 872. Bibcode:1957JChPh..26..872M. doi:10.1063/1.1743424.
- Marcus, R.A (1960). "Exchange reactions and electron transfer reactions including isotopic exchange. Theory of oxidation-reduction reactions involving electron transfer. Part 4.—A statistical-mechanical basis for treating contributions from solvent, ligands, and inert salt". Disc. Faraday Soc. 29: 21. doi:10.1039/df9602900021.
- Marcus, R.A (1963). "On The Theory Of Oxidation--Reduction Reactions Involving Electron Transfer. V. Comparison And Properties Of Electrochemical And Chemical Rate Constants". J. Phys. Chem. 67 (4): 853. doi:10.1021/j100798a033.
- Marcus, R.A (1964). "Chemical and Electrochemical Electron-Transfer Theory". Annu. Rev. Phys. Chem. 15 (1): 155. Bibcode:1964ARPC...15..155M. doi:10.1146/annurev.pc.15.100164.001103.
- Marcus, R.A (1965). "On the Theory of Electron-Transfer Reactions. VI. Unified Treatment for Homogeneous and Electrode Reactions". J. Chem. Phys. 43 (2): 679. Bibcode:1965JChPh..43..679M. doi:10.1063/1.1696792.
- Marcus, R.A.; Sutin N (1985). "Electron transfers in chemistry and biology". Biochim. Biophys. Acta 811 (3): 265. doi:10.1016/0304-4173(85)90014-X.
![\mathrm{D+A \ \overset{\xrightarrow{k_{12}}}{\xleftarrow[k_{21}]{}} \ [D{\dotsm}A] \ \overset{\xrightarrow{k_{23}}}{\xleftarrow[k_{32}]{}} \ [D^+{\dotsm}A^-] \xrightarrow{k_{30}} \ D^+ + A^-}](../I/m/1add8e2596eb247bd4510cfb3946644c.png)
![\mathrm{[Fe^{II}(CN)_{6}]^{4-}}+\mathrm{[Ir^{IV}Cl_{6}]^{2-}}\rightleftharpoons\mathrm{[Fe^{III}(CN)_{6}]^{3-}}+\mathrm{[Ir^{III}Cl_{6}]^{3-}}](../I/m/6d3dddb997279b98e0f48094bb48a054.png)
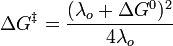
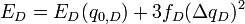
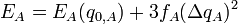
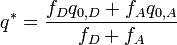
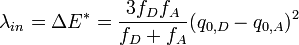
![\mathrm{[Fe(H_2O)_6]^{2+}} +\mathrm{[[Co(H_2O)_6]]^{3+}} \rightleftharpoons \mathrm{[Fe(H_2O)_6]^{3+}} + \mathrm{[Co(H_2O)_6]^{2+}}](../I/m/7ed32ecf10b594abe6eb62c5b7f9bec2.png)
![P_{if} = 1-\exp[-\frac{4\pi^2 {H_{if}^2}}{hv \mid(s_i - s_f)\mid}]](../I/m/fb05ddad222c5677722c84e7ae4b3f4f.png)