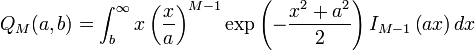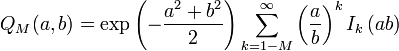Marcum Q-function

In statistics, the Marcum-Q-function 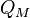$Q_M$ is defined as

Q_M (a,b) = \int_{b}^{\infty} x \left( \frac{x}{a}\right)^{M-1} \exp \left( -\frac{x^2 + a^2}{2} \right) I_{M-1} \left( a x \right) dx

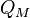$Q_M$ is also defined as

Q_M (a,b) = \exp \left( -\frac{a^2 + b^2}{2} \right) \sum_{k=1-M}^{\infty} \left( \frac{a}{b}\right)^{k} I_{k} \left( a b \right)

with modified Bessel function 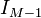$I_{M-1}$ of order M − 1. The Marcum Q-function is used for example as a cumulative distribution function for noncentral chi-squared and Rice distributions.

The Marcum Q-function is monotonic and log-concave.^[1]

References

Marcum, J. I. (1950) "Table of Q Functions". U.S. Air Force RAND Research Memorandum M-339. Santa Monica, CA: Rand Corporation, Jan. 1, 1950.
Nuttall, Albert H. (1975): Some Integrals Involving the Q_M Function, IEEE Transactions on Information Theory, 21(1), 95-96, ISSN 0018-9448
Weisstein, Eric W. Marcum Q-Function. From MathWorld—A Wolfram Web Resource.

↑ Yin Sun, Árpád Baricz, and Shidong Zhou (2010) On the Monotonicity, Log-Concavity, and Tight Bounds of the Generalized Marcum and Nuttall Q-Functions. IEEE Transactions on Information Theory, 56(3), 1166-1186, ISSN 0018-9448

This article is issued from Wikipedia - version of the Monday, April 22, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.