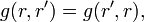Marchenko equation

In mathematical physics, more specific in the one-dimensional inverse scattering problem, the Marchenko equation, named after Vladimir Marchenko, is derived by computing the Fourier transform of the scattering relation:

K(r,r^\prime) + g(r,r^\prime) + \int_r^{\infty} K(r,r^{\prime\prime}) g(r^{\prime\prime},r^\prime) \mathrm{d}r^{\prime\prime} = 0

where

g(r,r^\prime)\,

is a symmetric kernel, so that

g(r,r^\prime)=g(r^\prime,r),\,

which is computed from the scattering data. Solving the Marchenko equation one obtains the kernel of the transformation operator 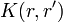$K(r,r^\prime)$ from which the potential can be read off.

This equation is derived from the Gel'fand-Levitan integral equation, using the Povzner-Levitan representation.

References

Marchenko, V. A. (2011), Sturm-Liouville operators and applications (2 ed.), Providence: American Mathematical Society, ISBN 978-0-8218-5316-0, MR 2798059 .

This article is issued from Wikipedia - version of the Friday, February 24, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.