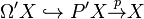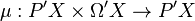Path space fibration
In algebraic topology, the path space fibration over a based space (X, *)[1] is a fibration of the form
where
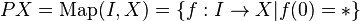 is the space called the path space of X.
is the space called the path space of X. is the fiber of
is the fiber of 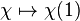 over the base point of X; thus it is the loop space of X.
over the base point of X; thus it is the loop space of X.
The space 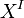 consists of all maps from I to X that may not preserve the base points; it is called the free path space of X and the fibration
consists of all maps from I to X that may not preserve the base points; it is called the free path space of X and the fibration 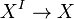 given by, say,
given by, say, 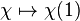 , is called the free path space fibration.
, is called the free path space fibration.
Mapping path space
If ƒ:X→Y is any map, then the mapping path space Pƒ of ƒ is the pullback of 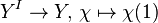 along ƒ. Since a fibration pullbacks to a fibration, if Y is based, one has the fibration
along ƒ. Since a fibration pullbacks to a fibration, if Y is based, one has the fibration
where 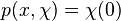 and
and  is the homotopy fiber, the pullback of
is the homotopy fiber, the pullback of 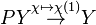 along ƒ.
along ƒ.
Note also ƒ is the composition
where the first map φ sends x to 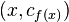 ,
, 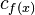 the constant path with value ƒ(x). Clearly, φ is a homotopy equivalence; thus, the above decomposition says that any map is a fibration up to homotopy equivalence.
the constant path with value ƒ(x). Clearly, φ is a homotopy equivalence; thus, the above decomposition says that any map is a fibration up to homotopy equivalence.
If ƒ is a fibration to begin with, then 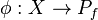 is a fiber-homotopy equivalence and, consequently,[2] the fibers of f over the path-component of the base point are homotopy equivalent to the homotopy fiber
is a fiber-homotopy equivalence and, consequently,[2] the fibers of f over the path-component of the base point are homotopy equivalent to the homotopy fiber  of ƒ.
of ƒ.
Moore's path space
By definition, a path in a space X is a map from the unit interval I to X. Again by definition, the product of two paths α, β such that α(1) = β(0) is the path β · α: I → X given by:
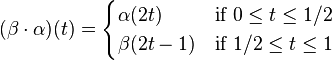 .
.
This product, in general, fails to be associative on the nose: (γ · β) · α ≠ γ · (β · α), as seen directly. One solution to this failure is to pass to homotopy classes: one has [(γ · β) · α ] = [γ · (β · α)]. Another solution is to work with paths of arbitrary length, leading to the notions of Moore's path space and Moore's path space fibration.[3]
Given a based space (X, *), we let
An element f of this set has the unique extension 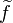 to the interval
to the interval  such that
such that 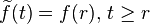 . Thus, the set can be identified as a subspace of
. Thus, the set can be identified as a subspace of 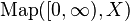 . The resulting space is called Moore's path space of X. Then, just as before, there is a fibration, Moore's path space fibration:
. The resulting space is called Moore's path space of X. Then, just as before, there is a fibration, Moore's path space fibration:
where p sends each f: [0, r] → X to f(r) and 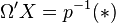 is the fiber. It turns out that
is the fiber. It turns out that  and
and 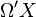 are homotopy equivalent.
are homotopy equivalent.
Now, we define the product map:
by: for ![f: [0, r] \to X](../I/m/a4476e97cd06b196fb05325304bb41f5.png) and
and ![g: [0, s] \to X](../I/m/4968050a3d723e41551d7225ea3e08bd.png) ,
,
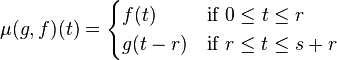 .
.
This product is manifestly associative. In particular, with μ restricted to Ω'X × Ω'X, we have that Ω'X is a topological monoid (in the category of all spaces). Moreover, this monoid Ω'X acts on P'X through the original μ. In fact, 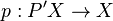 is an Ω'X-fibration.[4]
is an Ω'X-fibration.[4]
Notes
- ↑ Throughout the article, spaces are objects of the category of "reasonable" spaces; e.g., the category of compactly generated weak Haudsorff spaces.
- ↑ using the change of fiber
- ↑ Whitehead 1979, Ch. III, § 2.
- ↑ Let G = Ω'X and P = P'X. That G preserves the fibers is clear. To see, for each γ in P, the map
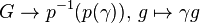 is a weak equivalence, we can use the following lemma:
Lemma — Let p: D → B, q: E → B be fibrations over an unbased space B, f: D → E a map over B. If B is path-connected, then the following are equivalent:We apply the lemma with
is a weak equivalence, we can use the following lemma:
Lemma — Let p: D → B, q: E → B be fibrations over an unbased space B, f: D → E a map over B. If B is path-connected, then the following are equivalent:We apply the lemma with- f is a weak equivalence.
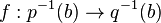 is a weak equivalence for some b in B.
is a weak equivalence for some b in B.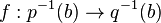 is a weak equivalence for every b in B.
is a weak equivalence for every b in B.
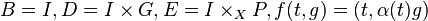 where α is a path in P and I → X is t → the end-point of α(t). Since
where α is a path in P and I → X is t → the end-point of α(t). Since 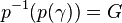 if γ is the constant path, the claim follows from the lemma. (In a nutshell, the lemma follows from the long exact homotopy sequence and the five lemma.)
if γ is the constant path, the claim follows from the lemma. (In a nutshell, the lemma follows from the long exact homotopy sequence and the five lemma.)
References
- James F. Davis, Paul Kirk, Lecture Notes in Algebraic Topology
- May, J. A Concise Course in Algebraic Topology
- George William Whitehead (1978). Elements of homotopy theory. Graduate Texts in Mathematics 61 (3rd ed.). New York-Berlin: Springer-Verlag. pp. xxi+744. ISBN 978-0-387-90336-1. MR 0516508. Retrieved September 6, 2011.
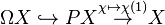
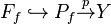
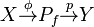
![P' X = \{ f: [0, r] \to X | r \ge 0, f(0) = * \}.](../I/m/b863a34caa299b3df683a3d04bcb4ef0.png)