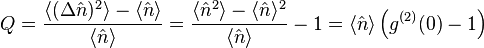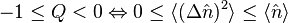Mandel Q parameter

The Mandel Q parameter measures the departure of the occupation number distribution from Poissonian statistics. It was introduced in quantum optics by L. Mandel.^[1] It is a convenient way to characterize non-classical states with negative values indicating a sub-Poissonian statistics, which have no classical analog. It is defined as the normalized variance of the boson distribution:

Q=\frac{\left \langle (\Delta \hat{n})^2 \right \rangle - \langle \hat{n} \rangle}{\langle \hat{n} \rangle} = \frac{\langle \hat{n}^2 \rangle - \langle \hat{n} \rangle^2}{\langle \hat{n} \rangle} -1 = \langle \hat{n} \rangle \left(g^{(2)}(0)-1 \right)

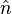where $\hat{n}$ is the photon number operator and 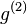$g^{(2)}$ is the normalized second-order correlation function as defined by Glauber.^[2]

Non-classical value

Negative values of Q corresponds to state which variance of photon number is less than the mean (equivalent to sub-Poissonian statistics). In this case, the phase space distribution cannot be interpreted as a classical probability distribution.

-1\leq Q < 0 \Leftrightarrow 0\leq \langle (\Delta \hat{n})^2 \rangle \leq \langle \hat{n} \rangle

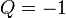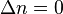The minimal value $Q=-1$ is obtained for photon number states, which by definition have a well-defined number of photon and for which $\Delta n=0$ .

Examples

For black-body radiation, the phase-space functional is Gaussian. The resulting occupation distribution of the number state is characterized by a Bose–Einstein statistics for which 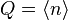$Q=\langle n\rangle$ .^[3]

Coherent states have a Poissonian photon-number statistics for which 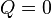$Q=0$ .

References

↑ Mandel, L., Sub-Poissonian photon statistics in resonance fluorescence, Opt. Lett. 4:205 (1979)
↑ Glauber, R. J., The Quantum Theory of Optical Coherence, Phys. Rev. 130:2529 (1963)
↑ Mandel, L., and Wolf, E., Optical Coherence and Quantum Optics (Cambridge 1995)

Mandel Q parameter

Non-classical value

Examples

References

Further reading