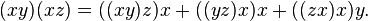Malcev algebra

In mathematics, a Malcev algebra (or Maltsev algebra or Moufang–Lie algebra) over a field is a nonassociative algebra that is antisymmetric, so that

and satisfies the Malcev identity

They were first defined by Anatoly Maltsev (1955).

Malcev algebras play a role in the theory of Moufang loops that generalizes the role of Lie algebras in the theory of groups. Namely, just as the tangent space of the identity element of a Lie group forms a Lie algebra, the tangent space of the identity of a smooth Moufang loop forms a Malcev algebra. Moreover, just as a Lie group can be recovered from its Lie algebra under certain supplementary conditions, a smooth Moufang loop can be recovered from its Malcev algebra if certain supplementary conditions hold. For example, this is true for a connected, simply connected real-analytic Moufang loop.^[1]

Examples

• Any Lie algebra is a Malcev algebra.
• Any alternative algebra may be made into a Malcev algebra by defining the Malcev product to be xy − yx.
• The 7-sphere may be given the structure of a smooth Moufang loop by identifying it with the unit octonions. The tangent space of the identity of this Moufang loop may be identified with the 7-dimensional space of imaginary octonions. The imaginary octonions form a Malcev algebra with the Malcev product xy − yx.

See also

• Malcev-admissible algebra

Notes

References

• Alberto Elduque and Hyo C. Myung Mutations of alternative algebras, Kluwer Academic Publishers, Boston, 1994, ISBN 0-7923-2735-7
• V.T. Filippov (2001), "Mal'tsev algebra", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 
• Mal'cev, A. I. (1955), "Analytic loops", Mat. Sb. N.S. (in Russian) 36 (78): 569–576, MR 0069190