Maker-Breaker game

In combinatorial game theory, Maker-Breaker games are a subclass of positional games.[1] [2]

It is a two-person game with complete information played on a hypergraph (V,H) where V is an arbitrary set (called the board of the game) and H is a family of subsets of V, called the winning sets. The two players alternately occupy previously unoccupied elements of V.

The first player, Maker, has to occupy a winning set to win; and the second player, Breaker, has to stop Maker from doing so; if Breaker successfully prevents maker from occupying a winning set to the end of the game, then Breaker wins. Thus, in a Maker–Breaker positional game, Maker wins if he occupies all elements of some winning set and Breaker wins if he prevents Maker from doing so. There can be no draw in a Maker-Breaker positional game: one player always wins.

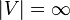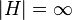The definition of Maker-Breaker game has a subtlety when |V|=\infty and |H|=\infty. In this case we say that Breaker has a winning strategy if, for all j > 0, Breaker can prevent Maker from completely occupying a winning set by turn j.

When tictactoe is played as a Maker–Breaker positional game, Maker has a winning strategy (Maker does not need to block Breaker from obtaining a winning line) .[3]

Maker-Breaker games on graphs

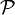There has been quite some research done on playing Maker-Breaker games when the board of the game is the edge-set of a graph G=(V,E) (usually taken as the complete graph) and the family of winning sets is \mathcal{F}=\{F\subset E\vert G[F]\hbox{ has property }\mathcal{P}\}, where \mathcal{P} is some graph property (usually taken to be monotone increasing) such as connectivity (see, e.g.,[4]).

References

  1. ↑ J. Beck: Combinatorial Games: Tic-Tac-Toe Theory, Cambridge University Press, 2008.
  2. ↑ D. Hefetz, M. Krivelevich, M. Stojaković and T. Szabó: Positional Games, Oberwolfach Seminars, Vol. 44, Birkhäuser Basel, 2014.
  3. ↑ Kruczek, Klay; Eric Sundberg (2010). "Potential-based strategies for tic-tac-toe on the integer latticed with numerous directions". The Electronic Journal of Combinatorics 17: R5.
  4. ↑ Chvatal; Erdos (1978). "Biased positional games". Annals of discrete mathematics 2: 221–229.
This article is issued from Wikipedia - version of the Sunday, January 31, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.