Inverse magnetostrictive effect

The inverse magnetostrictive effect (also known as magnetoelastic effect or Villari effect) is the name given to the change of the magnetic susceptibility of a material when subjected to a mechanical stress.

Explanation

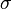The magnetostriction $\lambda$ characterizes the shape change of a ferromagnetic material during magnetization, whereas the inverse magnetostrictive effect characterizes the change of sample magnetization $M$ (for given magnetizing field strength $H$ ) when mechanical stresses $\sigma$ are applied to the sample.^[1]

Qualitative explanation of magnetoelastic effect

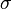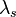Under a given uni-axial mechanical stress $\sigma$ , the flux density $B$ for a given magnetizing field strength $H$ may increase or decrease. The way in which a material responds to stresses depends on its saturation magnetostriction $\lambda_s$ . For this analysis, compressive stresses 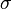$\sigma$ are considered as negative, whereas tensile stresses are positive.
According to Le Chatelier's principle:

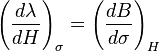
$\left(\frac{d\lambda}{dH}\right)_{\sigma}=\left(\frac{dB}{d\sigma}\right)_{H}$

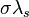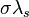This means, that when the product $\sigma \lambda_s$ is positive, the flux density $B$ increases under stress. On the other hand, when the product $\sigma \lambda_s$ is negative, the flux density $B$ decreases under stress. This effect was confirmed experimentally.^[2]

Quantitative explanation of magnetoelastic effect

In the case of a single stress 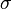$\sigma$ acting upon a single magnetic domain, the magnetic strain energy density 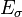$E_\sigma$ can be expressed as:^[1]

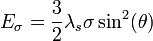
$E_\sigma = \frac{3}{2} \lambda_s \sigma \sin^2(\theta)$

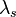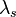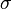where $\lambda_s$ is the magnetostrictive expansion at saturation, and $\theta$ is the angle between the saturation magnetization and the stress's direction. When $\lambda_s$ and $\sigma$ are both positive (like in iron under tension), the energy is minimum for $\theta$ = 0, i.e. when tension is aligned with the saturation magnetization. Consequently, the magnetization is increased by tension.

Magnetoelastic effect in the single crystal

In fact, magnetostriction is more complex and depends on the direction of the crystal axes. In iron, the [100] axes are the directions of easy magnetization, while there is little magnetization along the [111] directions (unless the magnetization becomes close to the saturation magnetization, leading to the change of the domain orientation from [111] to [100]). This magnetic anisotropy pushed authors to define two independent longitudinal magnetostrictions 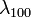$\lambda_{100}$ and $\lambda_{111}$ .

In cubic materials, the magnetostriction along any axis can be defined by a known linear combination of these two constants. For instance, the elongation along [110] is a linear combination of 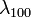$\lambda_{100}$ and $\lambda_{111}$ .
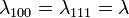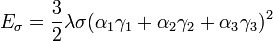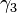Under assumptions of isotropic magnetostriction (i.e. domain magnetization is the same in any crystallographic directions), then $\lambda_{100} = \lambda_{111} = \lambda$ and the linear dependence between the elastic energy and the stress is conserved, $E_\sigma = \frac{3}{2} \lambda \sigma (\alpha_1 \gamma_1 +\alpha_2 \gamma_2 + \alpha_3 \gamma_3)^2$ . Here, $\alpha_1$ , $\alpha_2$ and $\alpha_3$ are the direction cosines of the domain magnetization, and $\gamma_1$ , $\gamma_2$ , $\gamma_3$ those of the bond directions, towards the crystallographic directions.

Method of testing the magnetoelastic properties of soft magnetic materials

Method suitable for effective testing of magnetoelastic effect in magnetic materials should fulfill the following requirements:^[3]

magnetic circuit of the tested sample should be closed. Open magnetic circuit causes demagnetization, which reduces magnetoelastic effect and complicates its analysis.
distribution of stresses should be uniform. Value and direction of stresses should be known.
there should be the possibility of making the magnetizing and sensing windings on the sample - necessary to measure magnetic hysteresis loop under mechanical stresses.

Following testing methods were developed:

tensile stresses applied to the strip of magnetic material in the shape of a ribbon.^[4] Disadvantage: open magnetic circuit of the tested sample.
tensile or compressive stresses applied to the frame-shaped sample.^[5] Disadvantage: only bulk materials may be tested. No stresses in the joints of sample columns.
compressive stresses applied to the ring core in the sideways direction.^[6] Disadvantage: non-uniform stresses distribution in the core .
tensile or compressive stresses applied axially to the ring sample.^[7] Disadvantage: stresses are perpendicular to the magnetizing field.

Applications of magnetoelastic effect

Magnetoelastic effect can be used in development of force sensors.^[8]^[9] This effect was used for sensors:

in civil engineering.^[4]
for monitoring of large diesel engines in locomotives.^[10]
for monitoring of ball valves.^[10]
for biomedical monitoring.^[11]

Magnetoelastic effect have to be also considered as a side effect of accidental application of mechanical stresses to the magnetic core of inductive component, e.g. fluxgates.^[12]

References

1 2 Bozorth, R. (1951). Ferromagnetism. Van Nostrand.
↑ Salach, J.; Szewczyk, R.; Bienkowski, A.; Frydrych, P. (2010). "Methodology of testing the magnetoelastic characteristics of ring-shaped cores under uniform compressive and tensile stresses" (PDF). Journal of Electrical Engineering 61 (7): 93.
↑ Bienkowski, A.; Kolano, R.; Szewczyk, R (2003). "New method of characterization of magnetoelastic properties of amorphous ring cores". Journal of Magnetism and Magnetic Materials 254: 67. Bibcode:2003JMMM..254...67B. doi:10.1016/S0304-8853(02)00755-2.
1 2 Bydzovsky, J.; Kollar, M.; Svec, P.; et al. (2001). "Magnetoelastic properties of CoFeCrSiB amorphous ribbons - a possitility of their application" (PDF). Journal of Electrical Engineering 52: 205.
↑ Bienkowski, A.; Rozniatowski, K.; Szewczyk, R (2003). "Effects of stress and its dependence on microstructure in Mn-Zn ferrite for power applications". Journal of Magnetism and Magnetic Materials 254: 547. Bibcode:2003JMMM..254..547B. doi:10.1016/S0304-8853(02)00861-2.
↑ Mohri, K.; Korekoda, S. (1978). "New force transducers using amorphous ribbon cores". IEEE Transactions on Magnetics 14: 1071. Bibcode:1978ITM....14.1071M. doi:10.1109/TMAG.1978.1059990.
↑ Szewczyk, R.; Bienkowski, A.; Salach, J.; et al. (2003). "The influence of microstructure on compressive stress characteristics of the FINEMET-type nanocrystalline sensors" (PDF). Journal of Optoelectronics and Advanced Materials 5: 705.
↑ Bienkowski, A.; Szewczyk, R. (2004). "The possibility of utilizing the high permeability magnetic materials in construction of magnetoelastic stress and force sensors". Sensors and Actuators A - Physical (Elsevier) 113: 270. doi:10.1016/j.sna.2004.01.010.
↑ Bienkowski, A.; Szewczyk, R. (2004). "New possibility of utilizing amorphous ring cores as stress sensor". Physica Status Solidi A - Applied Research 189: 787. Bibcode:2002PSSAR.189..787B. doi:10.1002/1521-396X(200202)189:3<787::AID-PSSA787>3.0.CO;2-G.
1 2 Bienkowski, A.; Szewczyk, R.; Salach, J. (2010). "Industrial Application of Magnetoelastic Force and Torque Sensors" (PDF). Acta Physica Polonica A 118: 1008.
↑ Meydan, T.; Oduncu, H. (1997). "Enhancement of magnetostrictive properties of amorphous ribbons for a biomedical application". Sensors and Actuators A - Physical (Elsevier) 59: 192. doi:10.1016/S0924-4247(97)80172-0.
↑ Szewczyk, R.; Bienkowski, A. (2004). "Stress dependence of sensitivity of fluxgate sensor". Sensors and Actuators A - Physical (Elsevier) 110 (1-3): 232. doi:10.1016/j.sna.2003.10.029.