Mach's principle
In theoretical physics, particularly in discussions of gravitation theories, Mach's principle (or Mach's conjecture[1]) is the name given by Einstein to an imprecise hypothesis often credited to the physicist and philosopher Ernst Mach. The idea is that local inertial frames are determined by the large scale distribution of matter, as exemplified by this anecdote:
You are standing in a field looking at the stars. Your arms are resting freely at your side, and you see that the distant stars are not moving. Now start spinning. The stars are whirling around you and your arms are pulled away from your body. Why should your arms be pulled away when the stars are whirling? Why should they be dangling freely when the stars don't move?
Mach's principle says that this is not a coincidence—that there is a physical law that relates the motion of the distant stars to the local inertial frame. If you see all the stars whirling around you, Mach suggests that there is some physical law which would make it so you would feel a centrifugal force. There are a number of rival formulations of the principle. It is often stated in vague ways, like "mass out there influences inertia here". A very general statement of Mach's principle is "Local physical laws are determined by the large-scale structure of the universe."[2]
This concept was a guiding factor in Einstein's development of the general theory of relativity. Einstein realized that the overall distribution of matter would determine the metric tensor, which tells you which frame is rotationally stationary. Frame dragging and conservation of gravitational angular momentum makes this into a true statement in the general theory in certain solutions. But because the principle is so vague, many distinct statements can be (and have been) made which would qualify as a Mach principle, and some of these are false. The Gödel rotating universe is a solution of the field equations which is designed to disobey Mach's principle in the worst possible way. In this example, the distant stars seem to be revolving faster and faster as one moves further away. This example doesn't completely settle the question, because it has closed timelike curves.
History
The basic idea also appears before Mach's time, in the writings of George Berkeley.[3] The book Absolute or Relative Motion? (1896) by Benedict Friedländer and his brother Immanuel contained ideas similar to Mach's principle.
Einstein's use of the principle
There is a fundamental issue in relativity theory. If all motion is relative, how can we measure the inertia of a body? We must measure the inertia with respect to something else. But what if we imagine a particle completely on its own in the universe? We might hope to still have some notion of its state of motion. Mach's principle is sometimes interpreted as the statement that such a particle's state of motion has no meaning in that case.
In Mach's words, the principle is embodied as follows:[4]
- [The] investigator must feel the need of... knowledge of the immediate connections, say, of the masses of the universe. There will hover before him as an ideal insight into the principles of the whole matter, from which accelerated and inertial motions will result in the same way.
Albert Einstein seemed to view Mach's principle as something along the lines of:[5]
- ...inertia originates in a kind of interaction between bodies...
In this sense, at least some of Mach's principles are related to philosophical holism. Mach's suggestion can be taken as the injunction that gravitation theories should be relational theories. Einstein brought the principle into mainstream physics while working on general relativity. Indeed, it was Einstein who first coined the phrase Mach's principle. There is much debate as to whether Mach really intended to suggest a new physical law since he never states it explicitly.
The writing in which Einstein found inspiration from Mach was "The Science of Mechanics", where the philosopher criticized Newton's idea of absolute space, in particular the argument that Newton gave sustaining the existence of an advantaged reference system: what is commonly called "Newton's bucket argument".
In his Philosophiae Naturalis Principia Mathematica, Newton tried to demonstrate that one can always decide if one is rotating with respect to the absolute space, measuring the apparent forces that arise only when an absolute rotation is performed. If a bucket is filled with water, and made to rotate, initially the water remains still, but then, gradually, the walls of the vessel communicate their motion to the water, making it curve and climb up the borders of the bucket, because of the centrifugal forces produced by the rotation. Newton says that this thought experiment demonstrates that the centrifugal forces arise only when the water is in rotation with respect to the absolute space (represented here by the earth's reference frame, or better, the distant stars); instead, when the bucket was rotating with respect to the water no centrifugal forces were produced, this indicating that the latter was still with respect to the absolute space.
Mach, in his book, says that the bucket experiment only demonstrates that when the water is in rotation with respect to the bucket no centrifugal forces are produced, and that we cannot know how the water would behave if in the experiment the bucket's walls were increased in depth and width until they became leagues big. In Mach's idea this concept of absolute motion should be substituted with a total relativism in which every motion, uniform or accelerated, has sense only in reference to other bodies (i.e., one cannot simply say that the water is rotating, but must specify if it's rotating with respect to the vessel or to the earth). In this view, the apparent forces that seem to permit discrimination between relative and "absolute" motions should only be considered as an effect of the particular asymmetry that there is in our reference system between the bodies which we consider in motion, that are small (like buckets), and the bodies that we believe are still (the earth and distant stars), that are overwhelmingly bigger and heavier than the former. This same thought had been expressed by the philosopher George Berkeley in his De Motu. It is then not clear, in the passages from Mach just mentioned, if the philosopher intended to formulate a new kind of physical action between heavy bodies. This physical mechanism should determine the inertia of bodies, in a way that the heavy and distant bodies of our universe should contribute the most to the inertial forces. More likely, Mach only suggested a mere "redescription of motion in space as experiences that do not invoke the term space".[6] What is certain is that Einstein interpreted Mach's passage in the former way, originating a long-lasting debate.
Most physicists believe Mach's principle was never developed into a quantitative physical theory that would explain a mechanism by which the stars can have such an effect. It was never made clear by Mach himself exactly what his principle was.[7] Although Einstein was intrigued and inspired by Mach's principle, Einstein's formulation of the principle is not a fundamental assumption of general relativity.
Mach's principle in general relativity
Because intuitive notions of distance and time no longer apply, what exactly is meant by "Mach's principle" in general relativity is even less clear than in Newtonian physics and at least 21 formulations of Mach's principle are possible, some being considered more strongly Machian than others.[8] A relatively weak formulation is the assertion that the motion of matter in one place should affect which frames are inertial in another.
Einstein—before completing his development of the general theory of relativity—found an effect which he interpreted as being evidence of Mach's principle. We assume a fixed background for conceptual simplicity, construct a large spherical shell of mass, and set it spinning in that background. The reference frame in the interior of this shell will precess with respect to the fixed background. This effect is known as the Lense–Thirring effect. Einstein was so satisfied with this manifestation of Mach's principle that he wrote a letter to Mach expressing this:
it... turns out that inertia originates in a kind of interaction between bodies, quite in the sense of your considerations on Newton's pail experiment... If one rotates [a heavy shell of matter] relative to the fixed stars about an axis going through its center, a Coriolis force arises in the interior of the shell; that is, the plane of a Foucault pendulum is dragged around (with a practically unmeasurably small angular velocity).[5]
The Lense–Thirring effect certainly satisfies the very basic and broad notion that "matter there influences inertia here"[9] The plane of the pendulum would not be dragged around if the shell of matter were not present, or if it were not spinning. As for the statement that "inertia originates in a kind of interaction between bodies", this too could be interpreted as true in the context of the effect.
More fundamental to the problem, however, is the very existence of a fixed background, which Einstein describes as "the fixed stars." Modern relativists see the imprints of Mach's principle in the Initial-Value Problem. Essentially, we humans seem to wish to separate spacetime into slices of constant time. When we do this, Einstein's equations can be decomposed into one set of equations, which must be satisfied on each slice, and another set, which describe how to move between slices. The equations for an individual slice are elliptic partial differential equations. In general, this means that only part of the geometry of the slice can be given by the scientist, while the geometry everywhere else will then be dictated by Einstein's equations on the slice.[Needs clarification]
In the context of an asymptotically flat spacetime, the boundary conditions are given at infinity. Heuristically, the boundary conditions for an asymptotically flat universe define a frame with respect to which inertia has meaning. By performing a Lorentz transformation on the distant universe, of course, this inertia can also be transformed.
A stronger form of Mach's principle applies in Wheeler-Mach-Einstein spacetimes, which require spacetime to be spatially compact and globally hyperbolic. In such universes Mach's principle can be stated as, 'the distribution of matter and field energy-momentum (and possibly other information) at a particular moment in the universe determines the inertial frame at each point in the universe' (where 'a particular moment in the universe' refers to a chosen Cauchy surface).[10]
There have been other attempts to formulate a theory which is more fully Machian, such as Brans–Dicke theory, but most physicists argue that none have been fully successful. At an exit poll of experts, held in Tübingen in 1993, when asked the question, 'Is general relativity perfectly Machian?', 3 respondents replied 'yes' and 22 replied 'no'. To the question, 'Is general relativity with appropriate boundary conditions of closure of some kind very Machian?' the result was 14 'yes' and 7 'no'.[11]
Variations in the statement of the principle
The broad notion that "mass there influences inertia here" has been expressed in several forms. Hermann Bondi and Joseph Samuel have listed eleven distinct statements which can be called Mach principles, labelled by Mach0 through Mach10.[12] Though their list is not necessarily exhaustive, it does give a flavor for the variety possible.
- Mach0: The universe, as represented by the average motion of distant galaxies, does not appear to rotate relative to local inertial frames.
- Mach1: Newton’s gravitational constant G is a dynamical field.
- Mach2: An isolated body in otherwise empty space has no inertia.
- Mach3: Local inertial frames are affected by the cosmic motion and distribution of matter.
- Mach4: The universe is spatially closed.
- Mach5: The total energy, angular and linear momentum of the universe are zero.
- Mach6: Inertial mass is affected by the global distribution of matter.
- Mach7: If you take away all matter, there is no more space.
- Mach8:
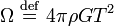 is a definite number, of order unity, where
is a definite number, of order unity, where  is the mean density of matter in the universe, and
is the mean density of matter in the universe, and  is the Hubble time.
is the Hubble time. - Mach9: The theory contains no absolute elements.
- Mach10: Overall rigid rotations and translations of a system are unobservable.
See also
References
- ↑ Hans Christian Von Bayer, The Fermi Solution: Essays on Science, Courier Dover Publications (2001), ISBN 0-486-41707-7, page 79
- ↑ Stephen W. Hawking & George Francis Rayner Ellis (1973). The Large Scale Structure of Space–Time. Cambridge University Press. p. 1. ISBN 0-521-09906-4.
- ↑ G. Berkeley (1726). The Principles of Human Knowledge. See paragraphs 111–117, 1710.
- ↑ Mach, Ernst (1960). The Science of Mechanics; a Critical and Historical Account of its Development. LaSalle, IL: Open Court Pub. Co. LCCN 60010179. This is a reprint of the English translation by Thomas H. MCormack (first published in 1906) with a new introduction by Karl Menger
- 1 2 A. Einstein, letter to Ernst Mach, Zurich, 25 June 1913, in Misner, Charles; Thorne, Kip S.; and Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. ISBN 0-7167-0344-0.
- ↑ Barbour, Julian; and Pfister, Herbert (eds.) (1995). Mach's principle: from Newton's bucket to quantum gravity. Boston: Birkhäuser. ISBN 3-7643-3823-7. (Einstein studies, vol. 6)
- ↑ Barbour, Julian; and Pfister, Herbert (eds.) (1995). Mach's principle: from Newton's bucket to quantum gravity. Boston: Birkhäuser. pp. 9–57. ISBN 3-7643-3823-7. (Einstein studies, vol. 6)
- ↑ Barbour, Julian; and Pfister, Herbert (eds.) (1995). Mach's principle: from Newton's bucket to quantum gravity. Boston: Birkhäuser. p. 530. ISBN 3-7643-3823-7. (Einstein studies, vol. 6)
- ↑ Bondi, Hermann & Samuel, Joseph (July 4, 1996). "The Lense–Thirring Effect and Mach's Principle". Physics Letters A 228 (3): 121. arXiv:gr-qc/9607009 [gr-qc]. Bibcode:1997PhLA..228..121B. doi:10.1016/S0375-9601(97)00117-5. A useful review explaining the multiplicity of "Mach principles" which have been invoked in the research literature (and elsewhere).
- ↑ Barbour, Julian; and Pfister, Herbert (eds.) (1995). Mach's principle: from Newton's bucket to quantum gravity. Boston: Birkhäuser. pp. 188–207. ISBN 3-7643-3823-7. (Einstein studies, vol. 6)
- ↑ Barbour, Julian; and Pfister, Herbert (eds.) (1995). Mach's principle: from Newton's bucket to quantum gravity. Boston: Birkhäuser. p. 106. ISBN 3-7643-3823-7. (Einstein studies, vol. 6)
- ↑ Bondi, Hermann; and Samuel, Joseph (July 4, 1996). "The Lense–Thirring Effect and Mach's Principle". arXiv:gr-qc/9607009. A useful review explaining the multiplicity of "Mach principles" which have been invoked in the research literature (and elsewhere).
Further reading
- Sciama, D. W. (1953). "On the Origin of Inertia". Royal Astronomical Society 113: 34. Bibcode:1953MNRAS.113...34S.
- Sciama, D. W. (1971). Modern Cosmology. Cambridge: Cambridge University Press. OCLC 6931707. This textbook, among other writings by Sciama, helped revive interest in Mach's principle.
- Raine, D. J. (1975). "Mach's Principle in general relativity". Royal Astronomical Society 171: 507. Bibcode:1975MNRAS.171..507R.
- Vishwakarma (2002). "A Machian Model of Dark Energy". Class.Quant.Grav. 19 (18): 4747–4752. arXiv:gr-qc/0205075. Bibcode:2002CQGra..19.4747V. doi:10.1088/0264-9381/19/18/309.
- Qadir, Asghar (2006). "Mach’s Principle, Black Holes and Quantum Relativity" (PDF). Asghar Qadir - Center for Advanced Mathematics and Physics (CAMP). National Center for Physics and National University of Sciences and Technology, Pakistan.
- Alexander Unzicker (2007). "A Look at the Abandoned Contributions to Cosmology of Dirac, Sciama and Dicke". Ann. Phys. (Berlin) 18: 57–70. arXiv:0708.3518. Bibcode:2009AnP...521...57U. doi:10.1002/andp.200810335.
- Pfister, Herbert; King, Markus (2015). Inertia and Gravitation. The Fundamental Nature and Structure of Space-Time. The Lecture Notes in Physics. Volume 897. Heidelberg: Springer. doi:10.1007/978-3-319-15036-9. ISBN 978-3-319-15035-2.
External links
| Wikibooks has more on the topic of: Mach's principle |
| Look up mach's principle in Wiktionary, the free dictionary. |
- Lists of Mach Principle related papers
- Relativity Science Calculator - From Galileo's Law of Inertia to Einstein's and Mach's Conjecture Principle of Inertia