Maass wave form

In mathematics, a Maass wave form or Maass form is a function on the upper half plane that transforms like a modular form but need not be holomorphic. They were first studied by Hans Maass in Maass (1949).

Definition

Let k be a half-integer, s be a complex number, and Γ be a discrete subgroup of SL₂(R). A Maass form of weight k for Γ with Laplace eigenvalue s is a smooth function from the upper half-plane to the complex numbers satisfying the following conditions:

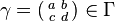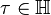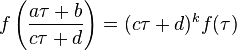For all $\gamma = \left(\begin{smallmatrix} a & b \\ c & d\end{smallmatrix}\right) \in \Gamma$ and all $\tau \in \mathbb{H}$ , we have $f\left(\frac{a\tau+b}{c\tau+d}\right) = (c\tau+d)^k f(\tau)$ .
We have 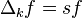$\Delta_{k} f = s f$ , where 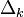$\Delta_{k}$ is the weight k hyperbolic laplacian defined as $\Delta_{k} = -y^{2} \left(\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}\right)+ i k y \frac{\partial}{\partial x}$ .
The function f is of at most polynomial growth at cusps.

A weak Maass wave form is defined similarly but with the third condition replaced by "The function f has at most linear exponential growth at cusps". Moreover, f is said to be harmonic if it is annihilated by the Laplacian operator.

Major Results

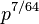Let $f$ be a weight 0 Maass cusp form. Its normalized Fourier coefficient at a prime $p$ is bounded by $p^{7/64}$ , due to Kim and Sarnak.

References

Bump, Daniel (1997), Automorphic forms and representations, Cambridge Studies in Advanced Mathematics 55, Cambridge University Press, ISBN 978-0-521-55098-7, MR 1431508
Maass, Hans (1949), "Über eine neue Art von nichtanalytischen automorphen Funktionen und die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen", Mathematische Annalen 121: 141–183, doi:10.1007/BF01329622, MR 0031519
K. Bringmann, A. Folsom, Almost harmonic Maass forms and Kac–Wakimoto characters, Crelle's Journal, Volume 2014, Issue 694, Pages 179–202 (2013). DOI: 10.1515/crelle-2012-0102
W. Duke, J. B. Friedlander and H. Iwaniec, The subconvexity problem for Artin L-Functions’', Inventiones Mathematicae, 149, pp. 489–577 (2002). Section 4. DOI: 10.1007/BF01329622.

This article is issued from Wikipedia - version of the Tuesday, December 22, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Maass wave form

Definition

Major Results

See also

References