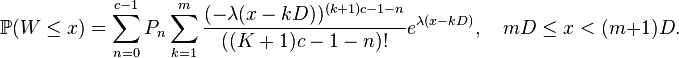M/D/c queue

In queueing theory, a discipline within the mathematical theory of probability, an M/D/c queue represents the queue length in a system having c servers, where arrivals are determined by a Poisson process and job service times are fixed (deterministic). The model name is written in Kendall's notation.^[1] Agner Krarup Erlang first published on this model in 1909, starting the subject of queueing theory.^[2]^[3] The model is an extension of the M/D/1 queue which has only a single server.

Model definition

An M/D/c queue is a stochastic process whose state space is the set {0,1,2,3,...} where the value corresponds to the number of customers in the system, including any currently in service.

Arrivals occur at rate λ according to a Poisson process and move the process from state i to i + 1.
Service times are deterministic time D (serving at rate μ = 1/D).
c servers serve customers from the front of the queue, according to a first-come, first-served discipline. When the service is complete the customer leaves the queue and the number of customers in the system reduces by one.
The buffer is of infinite size, so there is no limit on the number of customers it can contain.

Waiting time distribution

Erlang showed that when ρ = (λ D)/c < 1, the waiting time distribution has distribution F(y) given by^[4]

F(y) = \int_0^\infty F(x+y-D)\frac{\lambda^c x^{c-1}}{(c-1)!} e^{-\lambda x} \text{d} x, \quad y \geq 0 \quad c \in \mathbb N.

Crommelin showed that, writing P_n for the stationary probability of a system with n or fewer customers, ^[5]

\mathbb P(W \leq x) = \sum_{n=0}^{c-1} P_n \sum_{k=1}^m \frac{(-\lambda(x-kD))^{(k+1)c-1-n}}{((K+1)c-1-n)!}e^{\lambda(x-kD)}, \quad mD \leq x <(m+1)D.

References

↑ Kendall, D. G. (1953). "Stochastic Processes Occurring in the Theory of Queues and their Analysis by the Method of the Imbedded Markov Chain". The Annals of Mathematical Statistics 24 (3): 338. doi:10.1214/aoms/1177728975. JSTOR 2236285.
↑ Kingman, J. F. C. (2009). "The first Erlang century—and the next". Queueing Systems 63: 3–4. doi:10.1007/s11134-009-9147-4.
↑ "The theory of probabilities and telephone conversations" (PDF). Nyt Tidsskrift for Matematik B 20: 33–39. 1909. Archived from the original (PDF) on 2012-02-07.
↑ Franx, G. J. (2001). "A simple solution for the M/D/c waiting time distribution". Operations Research Letters 29 (5): 221–229. doi:10.1016/S0167-6377(01)00108-0.
↑ Crommelin, C.D. (1932). "Delay probability formulas when the holding times are constant". P.O. Electr. Engr. J. 25: 41–50.

Queueing theory

Single queueing nodes	D/M/1 queue M/D/1 queue M/D/c queue M/M/1 queue Burke's theorem M/M/c queue M/M/∞ queue M/G/1 queue Pollaczek–Khinchine formula Matrix analytic method M/G/k queue G/M/1 queue G/G/1 queue Kingman's formula Lindley equation Fork–join queue Bulk queue

Arrival processes	Poisson process Markovian arrival process Rational arrival process

Queueing networks	Jackson network Traffic equations Gordon–Newell theorem Mean value analysis Buzen's algorithm Kelly network G-network BCMP network

Service policies	FIFO LIFO Processor sharing Round-robin Shortest job first Shortest remaining time

Key concepts	Continuous-time Markov chain Kendall's notation Little's law Product-form solution Balance equation Quasireversibility Flow-equivalent server method Arrival theorem Decomposition method Beneš method

Limit theorems	Fluid limit Mean field theory Heavy traffic approximation Reflected Brownian motion

Extensions	Fluid queue Layered queueing network Polling system Adversarial queueing network Loss network Retrial queue

Information systems	Data buffer Erlang (unit) Erlang distribution Flow control (data) Message queue Network congestion Network scheduler Pipeline (software) Quality of service Scheduling (computing) Teletraffic engineering

Category

Stochastic processes

Discrete time	Bernoulli process Branching process Chinese restaurant process Galton–Watson process Independent and identically distributed random variables Markov chain Moran process Random walk Loop-erased Self-avoiding

Continuous time	Bessel process Birth–death process Brownian motion Bridge Excursion Fractional Geometric Meander Cauchy process Contact process Continuous-time random walk Cox process Diffusion process Empirical process Feller process Fleming–Viot process Gamma process Hunt process Interacting particle systems Itô diffusion Itô process Jump diffusion Jump process Lévy process Local time Markov additive process McKean–Vlasov process Ornstein–Uhlenbeck process Poisson process Compound Non-homogeneous Point process Schramm–Loewner evolution Semimartingale Sigma-martingale Stable process Superprocess Telegraph process Variance gamma process Wiener process Wiener sausage

Both	Branching process Gaussian process Hidden Markov model (HMM) Markov process Martingale Differences Local Sub- Super- Random dynamical system Regenerative process Renewal process White noise

Fields and other	Dirichlet process Gaussian random field Gibbs measure Hopfield model Ising model Potts model Boolean network Markov random field Percolation Pitman–Yor process Point process Cox Poisson Random field Random graph

Time series models	Autoregressive conditional heteroskedasticity (ARCH) model Autoregressive integrated moving average (ARIMA) model Autoregressive (AR) model Autoregressive–moving-average (ARMA) model Generalized autoregressive conditional heteroskedasticity (GARCH) model Moving-average (MA) model

Financial models	Black–Derman–Toy Black–Karasinski Black–Scholes Chen Constant elasticity of variance (CEV) Cox–Ingersoll–Ross (CIR) Garman–Kohlhagen Heath–Jarrow–Morton (HJM) Heston Ho–Lee Hull–White LIBOR market Rendleman–Bartter SABR volatility Vašíček Wilkie

Actuarial models	Bühlmann Cramér–Lundberg Risk process Sparre–Anderson

Queueing models	Bulk Fluid Generalized queueing network M/G/1 M/M/1 M/M/c

Properties	Càdlàg paths Continuous Continuous paths Ergodic Exchangeable Feller-continuous Gauss–Markov Markov Mixing Piecewise deterministic Predictable Progressively measurable Self-similar Stationary Time-reversible

Limit theorems	Central limit theorem Donsker's theorem Doob's martingale convergence theorems Ergodic theorem Fisher–Tippett–Gnedenko theorem Large deviation principle Law of large numbers (weak/strong) Law of the iterated logarithm Maximal ergodic theorem Sanov's theorem

Inequalities	Burkholder–Davis–Gundy Doob's martingale Kunita–Watanabe

Tools	Cameron–Martin formula Convergence of random variables Doléans-Dade exponential Doob decomposition theorem Doob–Meyer decomposition theorem Doob's optional stopping theorem Dynkin's formula Feynman–Kac formula Filtration Girsanov theorem Infinitesimal generator Itô integral Itô's lemma Kolmogorov continuity theorem Kolmogorov extension theorem Lévy–Prokhorov metric Malliavin calculus Martingale representation theorem Optional stopping theorem Prokhorov's theorem Quadratic variation Reflection principle Skorokhod integral Skorokhod's representation theorem Skorokhod space Snell envelope Stochastic differential equation Tanaka Stopping time Stratonovich integral Uniform integrability Usual hypotheses Wiener space Classical Abstract

Disciplines	Actuarial mathematics Econometrics Ergodic theory Extreme value theory (EVT) Large deviations theory Mathematical finance Mathematical statistics Probability theory Queueing theory Renewal theory Ruin theory Statistics Stochastic analysis Time series analysis Machine learning

List of topics Category

This article is issued from Wikipedia - version of the Saturday, August 29, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.