Lydersen method
The Lydersen method[1] is a group contribution method for the estimation of critical properties temperature (Tc), pressure (Pc) and volume (Vc). The Lydersen method is the prototype for and ancestor of many new models like Joback,[2] Klincewicz,[3] Ambrose,[4] Gani-Constantinou[5] and others.
The Lydersen method is based in case of the critical temperature on the Guldberg rule which establishes a relation between the normal boiling point and the critical temperature.
Equations
Critical temperature
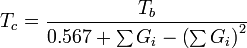
Guldberg has found that a rough estimate of the normal boiling point Tb, when expressed in kelvins (i.e., as an absolute temperature), is approximately two-thirds of the critical temperature Tc. Lydersen uses this basic idea but calculates more accurate values.
Critical pressure
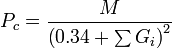
Critical volume
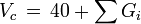
M is the molar mass and Gi are the group contributions (different for all three properties) for functional groups of a molecule.
Group contributions
| Group | Gi (Tc) | Gi (Pc) | Gi (Vc) | Group | Gi (Tc) | Gi (Pc) | Gi (Vc) |
|---|---|---|---|---|---|---|---|
| -CH3,-CH2- | 0.020 | 0.227 | 55.0 | >CH | 0.012 | 0.210 | 51.0 |
| -C< | - | 0,210 | 41.0 | =CH2,#CH | 0.018 | 0,198 | 45.0 |
| =C<,=C= | - | 0.198 | 36.0 | =C-H,#C- | 0.005 | 0.153 | 36.0 |
| -CH2-(Ring) | 0.013 | 0.184 | 44.5 | >CH-(Ring) | 0.012 | 0.192 | 46.0 |
| >C<(Ring) | -0.007 | 0.154 | 31.0 | =CH-,=C<,=C=(Ring) | 0.011 | 0.154 | 37.0 |
| -F | 0.018 | 0.224 | 18.0 | -Cl | 0.017 | 0.320 | 49.0 |
| -Br | 0.010 | 0.500 | 70.0 | -I | 0.012 | 0.830 | 95.0 |
| -OH | 0.082 | 0.060 | 18.0 | -OH(Aromat) | 0.031 | -0.020 | 3.0 |
| -O- | 0.021 | 0.160 | 20.0 | -O-(Ring) | 0.014 | 0.120 | 8.0 |
| >C=O | 0.040 | 0.290 | 60.0 | >C=O(Ring) | 0.033 | 0.200 | 50.0 |
| HC=O- | 0.048 | 0.330 | 73.0 | -COOH | 0.085 | 0.400 | 80.0 |
| -COO- | 0.047 | 0.470 | 80.0 | -NH2 | 0.031 | 0.095 | 28.0 |
| >NH | 0.031 | 0.135 | 37.0 | >NH(Ring) | 0.024 | 0.090 | 27.0 |
| >N | 0.014 | 0.170 | 42.0 | >N-(Ring) | 0.007 | 0.130 | 32.0 |
| -CN | 0.060 | 0.360 | 80.0 | -NO2 | 0.055 | 0.420 | 78.0 |
| -SH,-S- | 0.015 | 0.270 | 55.0 | -S-(Ring) | 0.008 | 0.240 | 45.0 |
| =S | 0.003 | 0.240 | 47.0 | >Si< | 0.030 | 0.540 | - |
| -B< | 0.030 | - | - |
Example calculation
Acetone is fragmented in two different groups, one carbonyl group and two methyl groups. For the critical volume the following calculation results:
Vc = 40 + 60.0 + 2 * 55.0 = 210 cm3
In the literature[6] the values 215.90 cm3,[7] 230.5 cm3 [8] and 209.0 cm3 [9] are published.
References
- ↑ Lydersen a.L., “Estimation of Critical Properties of Organic Compounds“, University of Wisconsin College Engineering, Eng. Exp. Stn. Rep. 3, Madison, Wisconsin
- ↑ Joback K.G., Reid R.C., “Estimation of pure-component properties from group-contributions”, Chem.Eng.Commun., 57, 233-243, 1987
- ↑ Klincewicz K. M., Reid R. C., "Estimation of Critical Properties with Group Contribution Methods", AIChE Journal, 30(1), 137-142, 1984
- ↑ Ambrose D., “Correlation and Estimation of Vapour-Liquid Critical Properties. I. Critical Temperatures of Organic Compounds”, Nat.Phys.Lab.Rep.Chem., Rep.No. 92, 1-35, 1978
- ↑ Constantinou L., Gani R., “New Group Contribution Method for Estimating Properties of Pure Compounds”, AIChE J., 40(10), 1697-1710, 1994
- ↑ Dortmund Data Bank
- ↑ Campbell A.N., Chatterjee R.M., Can.J.Chem., 47(20), S. 3893-3898, 1969
- ↑ Herz W., Neukirch E., Z.Phys.Chem.(Leipzig), 104, S.433-450, 1923
- ↑ Kobe K.A., Crawford H.R., Stephenson R.W., Ind.Eng.Chem., 47(9), S. 1767-1772, 1955