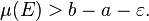Lusin's theorem
In the mathematical field of real analysis, Lusin's theorem (or Luzin's theorem, named for Nikolai Luzin) states that every measurable function is a continuous function on nearly all its domain. In the informal formulation of J. E. Littlewood, "every measurable function is nearly continuous".
Classical statement
For an interval [a, b], let
be a measurable function. Then, for every ε > 0, there exists a compact E ⊂ [a, b] such that f restricted to E is continuous and
Note that E inherits the subspace topology from [a, b]; continuity of f restricted to E is defined using this topology.
General form
Let  be a Radon measure space and Y be a second-countable topological space, let
be a Radon measure space and Y be a second-countable topological space, let
be a measurable function. Given ε > 0, for every 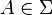 of finite measure there is a closed set E with µ(A \ E) < ε such that f restricted to E is continuous. If A is locally compact, we can choose E to be compact and even find a continuous function
of finite measure there is a closed set E with µ(A \ E) < ε such that f restricted to E is continuous. If A is locally compact, we can choose E to be compact and even find a continuous function 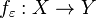 with compact support that coincides with f on E.
with compact support that coincides with f on E.
Informally, measurable functions into spaces with countable base can be approximated by continuous functions on arbitrarily large portion of their domain.
References
- N. Lusin. Sur les propriétés des fonctions mesurables, Comptes Rendus Acad. Sci. Paris 154 (1912), 1688–1690.
- G. Folland. Real Analysis: Modern Techniques and Their Applications, 2nd ed. Chapter 2
- W. Zygmunt. Scorza-Dragoni property (in Polish), UMCS, Lublin, 1990
![f:[a,b]\rightarrow \mathbb{C}](../I/m/7b94a3de27138fba7d5b93cde31d875c.png)