Lucas number

Not to be confused with Lucas sequences, a generic class of sequences to which the Lucas numbers belong.

The Lucas numbers or Lucas series are an integer sequence named after the mathematician François Édouard Anatole Lucas (1842–91), who studied both that sequence and the closely related Fibonacci numbers. Lucas numbers and Fibonacci numbers form complementary instances of Lucas sequences.

Definition

Similar to the Fibonacci numbers, each Lucas number is defined to be the sum of its two immediate previous terms, thereby forming a Fibonacci integer sequence. The first two Lucas numbers are L₀ = 2 and L₁ = 1 as opposed to the first two Fibonacci numbers F₀ = 0 and F₁ = 1. Though closely related in definition, Lucas and Fibonacci numbers exhibit distinct properties.

The Lucas numbers may thus be defined as follows:

L_n := \begin{cases} 2 & \text{if } n = 0; \\ 1 & \text{if } n = 1; \\ L_{n-1}+L_{n-2} & \text{if } n > 1. \\ \end{cases}

The sequence of Lucas numbers is:

2,\;1,\;3,\;4,\;7,\;11,\;18,\;29,\;47,\;76,\;123,\; \ldots\;

(sequence A000032 in OEIS).

All Fibonacci-like integer sequences appear in shifted form as a row of the Wythoff array; the Fibonacci sequence itself is the first row and the Lucas sequence is the second row. Also like all Fibonacci-like integer sequences, the ratio between two consecutive Lucas numbers converges to the golden ratio.

Extension to negative integers

Using L_n−2 = L_n − L_n−1, one can extend the Lucas numbers to negative integers to obtain a doubly infinite sequence:

..., −11, 7, −4, 3, −1, 2, 1, 3, 4, 7, 11, ... (terms

L_n

for

-5\leq{}n\leq5

are shown).

The formula for terms with negative indices in this sequence is

L_{-n}=(-1)^nL_n.\!

Relationship to Fibonacci numbers

The Lucas numbers are related to the Fibonacci numbers by the identities

$\,L_n = F_{n-1}+F_{n+1}=F_n+2F_{n-1} = F_{n+2}-F_{n-2}$
$\,L_{m+n} = L_{m+1}F_{n}+L_mF_{n-1}$
$\,L_n^2 = 5 F_n^2 + 4 (-1)^n$ , and thus as $n\,$ approaches +∞, the ratio $\frac{L_n}{F_n}$ approaches $\sqrt{5}.$
$\,F_{2n} = L_n F_n$
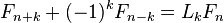
$\,F_{n+k} + (-1)^k F_{n-k} = L_k F_n$
$\,F_n = {L_{n-1}+L_{n+1} \over 5} = {L_{n-3}+L_{n+3} \over 10}$

Their closed formula is given as:

L_n = \varphi^n + (1-\varphi)^{n} = \varphi^n + (- \varphi)^{- n}=\left({ 1+ \sqrt{5} \over 2}\right)^n + \left({ 1- \sqrt{5} \over 2}\right)^n\, ,

where $\varphi$ is the golden ratio. Alternatively, as for $n>1$ the magnitude of the term $(-\varphi)^{-n}$ is less than 1/2, $L_n$ is the closest integer to $\varphi^n$ or, equivalently, the integer part of $\varphi^n+1/2$ , also written as $\lfloor \varphi^n+1/2 \rfloor$ .

Conversely, since Binet's formula gives:

F_n = \frac{\varphi^n - (1-\varphi)^{n}}{\sqrt{5}}\, ,

we have:

\varphi^n = {{L_n + F_n \sqrt{5}} \over 2}\, .

Congruence relations

If F_n ≥ 5 is a Fibonacci number then no Lucas number is divisible by F_n.

L_n is congruent to 1 mod n if n is prime, but some composite values of n also have this property.

Lucas primes

A Lucas prime is a Lucas number that is prime. The first few Lucas primes are

2, 3, 7, 11, 29, 47, 199, 521, 2207, 3571, 9349, 3010349, 54018521, 370248451, 6643838879, ... (sequence A005479 in OEIS).

For these ns are

0, 2, 4, 5, 7, 8, 11, 13, 16, 17, 19, 31, 37, 41, 47, 53, 61, 71, 79, 113, 313, 353, 503, 613, 617, 863, 1097, 1361, 4787, 4793, 5851, 7741, 8467, ... (sequence A001606 in OEIS).

If L_n is prime then n is either 0, prime, or a power of 2.^[1] L_2^m is prime for m = 1, 2, 3, and 4 and no other known values of m.

Lucas polynomials

In the same way as Fibonacci polynomials are derived from the Fibonacci numbers, the Lucas polynomials L_n(x) are a polynomial sequence derived from the Lucas numbers.

References

↑ Chris Caldwell, "The Prime Glossary: Lucas prime" from The Prime Pages.

External links

Hazewinkel, Michiel, ed. (2001), "Lucas polynomials", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Weisstein, Eric W., "Lucas Number", MathWorld.
Weisstein, Eric W., "Lucas Polynomial", MathWorld.
Dr Ron Knott
Lucas numbers and the Golden Section
A Lucas Number Calculator can be found here.
(sequence A000032 in OEIS) Lucas Numbers in the On-Line Encyclopedia of Integer Sequences.

Prime number classes

By formula	Fermat (2^2ⁿ + 1) Mersenne (2^p − 1) Double Mersenne (2^{2^p−1} − 1) Wagstaff (2^p + 1)/3 Proth (k·2ⁿ + 1) Factorial (n! ± 1) Primorial (p_n# ± 1) Euclid (p_n# + 1) Pythagorean (4n + 1) Pierpont (2^u·3^v + 1) Quartan (x⁴ + y⁴) Solinas (2^a ± 2^b ± 1) Cullen (n·2ⁿ + 1) Woodall (n·2ⁿ − 1) Cuban (x³ − y³)/(x − y) Carol (2ⁿ − 1)² − 2 Kynea (2ⁿ + 1)² − 2 Leyland (x^y + y^x) Thabit (3·2ⁿ − 1) Mills (floor(A^3ⁿ))

By integer sequence	Fibonacci Lucas Pell Newman–Shanks–Williams Perrin Partitions Bell Motzkin

By property	Wieferich (pair) Wall–Sun–Sun Wolstenholme Wilson Lucky Fortunate Ramanujan Pillai Regular Strong Stern Supersingular (elliptic curve) Supersingular (moonshine theory) Good Super Higgs Highly cototient

Base-dependent	Happy Dihedral Palindromic Emirp Repunit (10ⁿ − 1)/9 Permutable Circular Truncatable Strobogrammatic Minimal Weakly Full reptend Unique Primeval Self Smarandache–Wellin

Patterns	Twin (p, p + 2) Bi-twin chain (n − 1, n + 1, 2n − 1, 2n + 1, …) Triplet (p, p + 2 or p + 4, p + 6) Quadruplet (p, p + 2, p + 6, p + 8) k−Tuple Cousin (p, p + 4) Sexy (p, p + 6) Chen Sophie Germain (p, 2p + 1) Cunningham chain (p, 2p ± 1, …) Safe (p, (p − 1)/2) Arithmetic progression (p + a·n, n = 0, 1, …) Balanced (consecutive p − n, p, p + n)

By size	Titanic (1,000+ digits) Gigantic (10,000+) Mega (1,000,000+) Largest known

Complex numbers	Eisenstein prime Gaussian prime

Composite numbers	Pseudoprime Almost prime Semiprime Interprime

Related topics	Probable prime Industrial-grade prime Illegal prime Formula for primes Prime gap

First 100 primes	2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541

List of prime numbers

Classes of natural numbers

Powers and
related numbers

Of the form
a × 2^b ± 1

Other polynomial
numbers

Recursively defined
numbers

Possessing a
specific set
of other numbers

Expressible via
specific sums

Generated
via a sieve

Lucky

Code related

Meertens

Figurate numbers

2-dimensional

centered	Centered triangular Centered square Centered pentagonal Centered hexagonal Centered heptagonal Centered octagonal Centered nonagonal Centered decagonal Star

non-centered	Triangular Square Square triangular Pentagonal Hexagonal Heptagonal Octagonal Nonagonal Decagonal Dodecagonal

3-dimensional

centered	Centered tetrahedral Centered cube Centered octahedral Centered dodecahedral Centered icosahedral

non-centered	Tetrahedral Octahedral Dodecahedral Icosahedral Stella octangula

pyramidal	Square pyramidal Pentagonal pyramidal Hexagonal pyramidal Heptagonal pyramidal

4-dimensional

centered	Centered pentachoric Squared triangular

non-centered	Pentatope

Pseudoprimes

Combinatorial
numbers

Arithmetic functions

By properties of σ(n)	Abundant Almost perfect Arithmetic Colossally abundant Descartes Hemiperfect Highly abundant Highly composite Hyperperfect Multiply perfect Perfect Practical number Primitive abundant Quasiperfect Refactorable Sublime Superabundant Superior highly composite Superperfect

By properties of Ω(n)	Almost prime Semiprime

By properties of φ(n)	Highly cototient Highly totient Noncototient Nontotient Perfect totient Sparsely totient

By properties of s(n)	Amicable Betrothed Deficient Semiperfect

Dividing a quotient

Other prime factor
or divisor related
numbers

Recreational
mathematics

Base-dependent
numbers

This article is issued from Wikipedia - version of the Wednesday, November 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.