Lower convex envelope

In mathematics, the lower convex envelope 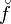\breve f of a function f defined on an interval [a,b] is defined at each point of the interval as the supremum of all convex functions that lie under that function, i.e.

f(x) = \sup\{ g(x) \mid g \text{ is convex and } g \leq f \text{ over } [a,b] \}.

See also

This article is issued from Wikipedia - version of the Thursday, December 24, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.