Lovász number
In graph theory, the Lovász number of a graph is a real number that is an upper bound on the Shannon capacity of the graph. It is also known as Lovász theta function and is commonly denoted by ϑ(G). This quantity was first introduced by László Lovász in his 1979 paper On the Shannon Capacity of a Graph.[1]
Definition
Let G = (V, E) be a graph on n vertices. An ordered set of n unit vectors U = (ui | i ∈ V) ⊂ RN is called an orthonormal representation of G in RN, if ui and uj are orthogonal whenever vertices i and j are not adjacent in G:
Clearly, every graph admits an orthonormal representation with N = n (just represent vertices by distinct vectors from the standard basis of Rn, though this will not in general be faithful unless the graph is edgeless; a faithful representation in N=n is also possible by associating each vertex to a basis vector as before, but mapping each vertex to the sum of basis vectors associated with its neighbourhood), but in general it might be possible to take N considerably smaller than the number of vertices n.
The Lovász number ϑ of graph G is defined as follows:
where c is a unit vector in RN and U is an orthonormal representation of G in RN. Here minimization implicitly is performed also over the dimension N, however without loss of generality it suffices to consider N = n.[2] Intuitively, this corresponds to minimizing the half-angle of a rotational cone containing all representing vectors of an orthonormal representation of G. If the optimal angle is ϕ, then ϑ(G) = 1/cos2(ϕ) and c corresponds to the symmetry axis of the cone.[3]
Equivalent expressions
Let G = (V, E) be a graph on n vertices. Let A range over all n × n symmetric matrices such that aij = 1 whenever i = j or ij ∉ E, and let λmax(A) denote the largest eigenvalue of A. Then an alternative way of computing the Lovász number of G is as follows:[4]
The following method is dual to the previous one. Let B range over all n × n symmetric positive semidefinite matrices such that bij = 0 for every ij ∈ E and Tr(B) = 1. Here Tr denotes trace (the sum of diagonal entries) and J is the n × n matrix of ones. Then[5]
Tr(BJ) is just the sum of all entries of B.
The Lovász number can be computed also in terms of the complement graph G. Let d be a unit vector and V = (vi | i ∈ V) be an orthonormal representation of G. Then[6]
Value of ϑ for some well-known graphs
| Graph | Value of ϑ[7] |
|---|---|
| Complete graph | 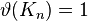 |
| Empty graph | 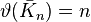 |
| Pentagon graph |  |
| Cycle graphs | 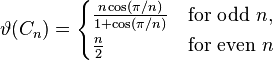 |
| Petersen graph | 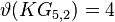 |
| Kneser graphs |  |
| Complete multipartite graphs | 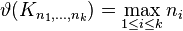 |
Properties
If G ⊠ H denotes the strong graph product of graphs G and H, then[8]
If G is the complement of G, then[9]
with equality if G is vertex-transitive.
Lovász "sandwich theorem"
The Lovász "sandwich theorem" states that the Lovász number always lies between two other numbers that are NP-complete to compute.[10] More precisely,
where ω(G) is the clique number of G (the size of the largest clique) and χ(G) is the chromatic number of G (the smallest number of colors needed to color the vertices of G so that no two adjacent vertices receive the same color). However, the value of ϑ(G) can be approximated by the ellipsoid method in time bounded by a polynomial in the number of vertices of G.[11]
Relation to Shannon capacity
The Shannon capacity of graph G is defined as follows:
where α(G) is the independence number of graph G (the size of a largest independent set of G) and Gk is the strong graph product of G with itself k times. Clearly, Θ(G) ≥ α(G). However, the Lovász number provides an upper bound on the Shannon capacity of graph,[12] hence

For example, let the confusability graph of the channel be C5, a pentagon. Since the original paper of Shannon (1956) it was an open problem to determine the value of Θ(C5). It was first established by Lovász (1979) that Θ(C5) = √5.
Clearly, Θ(C5) ≥ α(C5) = 2. However, α(C52) ≥ 5, since "11", "23", "35", "54", "42" are five mutually non-confusable messages (forming a five-vertex independent set in the strong square of C5), thus Θ(C5) ≥ √5.
To show that this bound is tight, let U = (u1, ..., u5) be the following orthonormal representation of the pentagon:
and let c = (1, 0, 0). By using this choice in the initial definition of Lovász number, we get ϑ(C5) ≤ √5. Hence, Θ(C5) = √5.
However, there exist graphs for which the Lovász number and Shannon capacity differ, so the Lovász number cannot in general be used to compute exact Shannon capacities.[13]
Quantum physics
The Lovász number has been generalized for "non-commutative graphs" in the context of quantum communication.[14] The Lovasz number also arises in quantum contextuality in an attempt to explain the power of quantum computers.[15]
Notes
- ↑ Lovász (1979).
- ↑ If N > n then one can always achieve a smaller objective value by restricting c to the subspace spanned by vectors ui which is at most n-dimensional.
- ↑ See Proposition 5.1 in Lovász (1995–2001), pp. 28.
- ↑ See Theorem 3 in Lovász (1979).
- ↑ See Theorem 4 in Lovász (1979).
- ↑ See Theorem 5 in Lovász (1979).
- ↑ Riddle (2003).
- ↑ See Lemma 2 and Theorem 7 in Lovász (1979).
- ↑ See Corollary 2 and Theorem 8 in Lovász (1979).
- ↑ Knuth (1994).
- ↑ Grötschel, Lovász & Schrijver (1981).
- ↑ See Theorem 1 in Lovász (1979).
- ↑ Haemers (1979).
- ↑ Duan, Severini & Winter (2010).
- ↑ Howard, Mark; Wallman, Joel; Veitch, Victor; Emerson, Joseph (19 June 2014), "Contextuality supplies the 'magic' for quantum computation", Nature 510: 351, doi:10.1038/nature13460
References
- Duan, Runyao; Severini, Simone; Winter, Andreas (2013) [2010], "Zero-error communication via quantum channels, non-commutative graphs and a quantum Lovász ϑ function", IEEE Trans. Inf. Theory 59 (2): 1164–1174, arXiv:1002.2514, doi:10.1109/TIT.2012.2221677.
- Grötschel, Martin; Lovász, László; Schrijver, Alexander (1981), "The ellipsoid method and its consequences in combinatorial optimization" (PDF), Combinatorica 1 (2): 169–197, doi:10.1007/BF02579273.
- Grötschel, Martin; Lovász, László; Schrijver, Alexander (1988), Geometric Algorithms and Combinatorial Optimization (2 ed.), Springer, ISBN 978-0-387-13624-0, Chapter 9.3. Orthonormal Representations, pp. 285.
- Haemers, Willem H. (1979), "On Some Problems of Lovász Concerning the Shannon Capacity of a Graph", IEEE Transactions on Information Theory 25: 231–232, doi:10.1109/tit.1979.1056027.
- Knuth, Donald E. (1994), "The sandwich theorem" (PDF), Electronic Journal of Combinatorics: A1, arXiv:math/9312214.
- Lovász, László (1979), "On the Shannon Capacity of a Graph", IEEE Transactions on Information Theory, IT-25 (1), doi:10.1109/tit.1979.1055985.
- Lovász, László (1986), An Algorithmic Theory of Numbers, Graphs and Convexity, SIAM, ISBN 978-0-89871-203-2, Chapter 3.2. Chromatic number, cliques, and perfect graphs, pp. 75.
- Lovász, László (1995–2001), Semidefinite programs and combinatorial optimization, lecture notes.
- Shannon, Claude (1956), "The zero error capacity of a noisy channel", IRE Transactions on Information Theory 2 (3): 8–19, doi:10.1109/TIT.1956.1056798.
External links
- Weisstein, Eric W., "Lovász Number", MathWorld.
- Weisstein, Eric W., "Sandwich Theorem", MathWorld.
- Weisstein, Eric W., "Shannon Capacity", MathWorld.
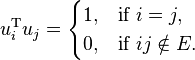
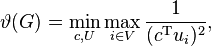
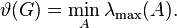
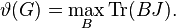
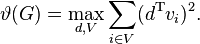

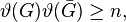
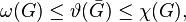
![\Theta(G)
= \sup_k \sqrt[k]{\alpha(G^k)}
= \lim_{k \rightarrow \infty} \sqrt[k]{\alpha(G^k)},](../I/m/fe076c7f83a2cb6fc42ec9b26c7e1e86.png)
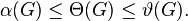
![u_k =
\begin{pmatrix}
\cos{\theta} \\
\sin{\theta} \cos{\varphi_k} \\
\sin{\theta} \sin{\varphi_k}
\end{pmatrix}, \quad
\cos{\theta} = \frac{1}{\sqrt[4]{5}}, \quad
\varphi_k = \frac{2 \pi k}{5}](../I/m/bfdf0939f66fa51c764275fd7d9e33b3.png)