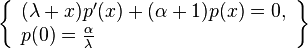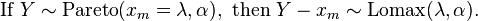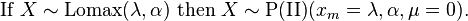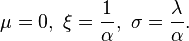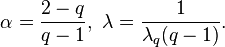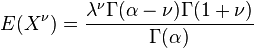Lomax distribution

Lomax
Parameters	$\lambda >0$ scale (real) $\alpha > 0$ shape (real)
Support	$x \ge 0$
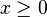PDF	${\alpha \over \lambda} \left[{1+ {x \over \lambda}}\right]^{-(\alpha+1)}$
CDF	$1- \left[{1+ {x \over \lambda}}\right]^{-\alpha}$
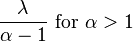Mean	${\lambda \over {\alpha -1}} \text{ for } \alpha > 1$ Otherwise undefined
Median	$\lambda (\sqrt[\alpha]{2} - 1)$
Mode	0
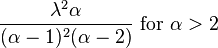Variance	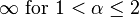${{\lambda^2 \alpha} \over {(\alpha-1)^2(\alpha-2)}} \text{ for } \alpha > 2$ $\infty \text{ for } 1 < \alpha \le 2$ Otherwise undefined
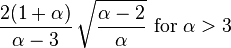Skewness	$\frac{2(1+\alpha)}{\alpha-3}\,\sqrt{\frac{\alpha-2}{\alpha}}\text{ for }\alpha>3\,$
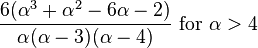Ex. kurtosis	$\frac{6(\alpha^3+\alpha^2-6\alpha-2)}{\alpha(\alpha-3)(\alpha-4)}\text{ for }\alpha>4\,$

The Lomax distribution, conditionally also called the Pareto Type II distribution, is a heavy-tail probability distribution often used in business, economics, and actuarial modeling.^[1]^[2] It is named after K. S. Lomax. It is essentially a Pareto distribution that has been shifted so that its support begins at zero.^[3]

Characterization

Probability density function

The probability density function (pdf) for the Lomax distribution is given by

p(x) = {\alpha \over \lambda} \left[{1+ {x \over \lambda}}\right]^{-(\alpha+1)}, \qquad x \geq 0,

with shape parameter $\alpha>0$ and scale parameter $\lambda>0$ . The density can be rewritten in such a way that more clearly shows the relation to the Pareto Type I distribution. That is:

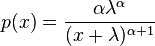p(x) = {{\alpha \lambda^\alpha} \over { (x+\lambda)^{\alpha+1}}}

Differential equation

The pdf of the Lomax distribution is a solution to the following differential equation:

\left\{\begin{array}{l} (\lambda +x) p'(x)+(\alpha +1) p(x)=0, \\ p(0)=\frac{\alpha}{\lambda} \end{array}\right\}

Relation to the Pareto distribution

The Lomax distribution is a Pareto Type I distribution shifted so that its support begins at zero. Specifically:

\text{If } Y \sim \mbox{Pareto}(x_m = \lambda, \alpha), \text{ then } Y - x_m \sim \mbox{Lomax}(\lambda,\alpha).

The Lomax distribution is a Pareto Type II distribution with x_m=λ and μ=0:^[4]

\text{If } X \sim \mbox{Lomax}(\lambda,\alpha) \text{ then } X \sim \text{P(II)}(x_m = \lambda, \alpha, \mu=0).

Relation to generalized Pareto distribution

The Lomax distribution is a special case of the generalized Pareto distribution. Specifically:

\mu = 0,~ \xi = {1 \over \alpha},~ \sigma = {\lambda \over \alpha} .

Relation to q-exponential distribution

The Lomax distribution is a special case of the q-exponential distribution. The q-exponential extends this distribution to support on a bounded interval. The Lomax parameters are given by:

\alpha = { {2-q} \over {q-1}}, ~ \lambda = {1 \over \lambda_q (q-1)} .

Non-central moments

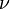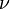The $\nu$ th non-central moment $E[X^\nu]$ exists only if the shape parameter $\alpha$ strictly exceeds $\nu$ , when the moment has the value

E(X^\nu) = \frac{ \lambda^\nu \Gamma(\alpha-\nu)\Gamma(1+\nu)}{\Gamma(\alpha)}

References

↑ Lomax, K. S. (1954) "Business Failures; Another example of the analysis of failure data". Journal of the American Statistical Association, 49, 847–852. JSTOR 2281544
↑ Johnson, N.L., Kotz, S., Balakrishnan, N. (1994) Continuous Univariate Distributions, Volume 1, 2nd Edition, Wiley. ISBN 0-471-58495-9 (pages 575, 602)
↑ Van Hauwermeiren M and Vose D (2009). A Compendium of Distributions [ebook]. Vose Software, Ghent, Belgium. Available at www.vosesoftware.com. Accessed 07/07/11
↑ Kleiber, Christian; Kotz, Samuel (2003), Statistical Size Distributions in Economics and Actuarial Sciences, Wiley Series in Probability and Statistics 470, John Wiley & Sons, p. 60, ISBN 9780471457169 .

Probability distributions

Discrete univariate with finite support

Benford Bernoulli Beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher discrete uniform Zipf Zipf–Mandelbrot

Discrete univariate with infinite support

beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta

Continuous univariate supported on a bounded interval, e.g. [0,1]

Arcsine ARGUS Balding–Nichols Bates Beta Beta rectangular Irwin–Hall Kumaraswamy logit-normal Noncentral beta raised cosine Reciprocal Triangular U-quadratic uniform Wigner semicircle

[[List of probability distributions#Supported_on_semi-infinite_intervals.2C_usually_.5B0.2C.E2.88.9E.29|Continuous univariate supported on a semi-infinite interval, usually [0,∞)]]

Continuous univariate supported on the whole real line (−∞, ∞)

Cauchy exponential power Fisher's z generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson S_U Landau Laplace Asymmetric Laplace Linnik logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel Tracy–Widom variance-gamma Voigt

Continuous univariate with support whose type varies

generalized extreme value generalized Pareto Tukey lambda q-Gaussian q-exponential q-Weibull shifted log-logistic

Mixed continuous-discrete univariate distributions

rectified Gaussian

Multivariate (joint)

Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet Generalized Dirichlet multivariate normal Multivariate stable multivariate Student normal-scaled inverse gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart

Directional

Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped asymmetric Laplace wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham

Degenerate and singular

Degenerate discrete degenerate Dirac delta function Singular Cantor

Families

Circular compound Poisson elliptical exponential natural exponential location-scale maximum entropy mixture Pearson Tweedie wrapped

This article is issued from Wikipedia - version of the Saturday, February 07, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.