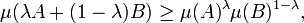Logarithmically concave measure

In mathematics, a Borel measure μ on n-dimensional Euclidean space Rn is called logarithmically concave (or log-concave for short) if, for any compact subsets A and B of Rn and 0 < λ < 1, one has

\mu(\lambda A + (1-\lambda) B) \geq \mu(A)^\lambda \mu(B)^{1-\lambda},

where λ A + (1 − λ) B denotes the Minkowski sum of λ A and (1 − λ) B.[1]

Examples

The Brunn–Minkowski inequality asserts that the Lebesgue measure is log-concave. The restriction of the Lebesgue measure to any convex set is also log-concave.

By a theorem of Borell,[2] a measure is log-concave if and only if it has a density with respect to the Lebesgue measure on some affine hyperplane, and this density is a logarithmically concave function. Thus, any Gaussian measure is log-concave.

The Prékopa–Leindler inequality shows that a convolution of log-concave measures is log-concave.

References

  1. ↑ Prékopa, A. (1980). "Logarithmic concave measures and related topics". Stochastic programming (Proc. Internat. Conf., Univ. Oxford, Oxford, 1974). London-New York: Academic Press. pp. 63–82. MR 0592596.
  2. ↑ Borell, C. (1975). "Convex set functions in d-space". Period. Math. Hungar. 6 (2): 111–136. doi:10.1007/BF02018814. MR 0404559.
This article is issued from Wikipedia - version of the Sunday, March 09, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.