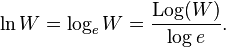Logarithmic units
Logarithmic units are abstract mathematical units that can be used to express any quantities (physical or mathematical) that are defined on a logarithmic scale, that is, as being proportional to the value of a logarithm function. In this article, a given logarithmic unit will be denoted using the notation [log n], where n is a positive real number, and [log ] here denotes the indefinite logarithm function Log().
Examples
Examples of logarithmic units include common units of information and entropy, such as the bit [log 2] and the byte 8[log 2] = [log 256], also the nat [log e] and the ban [log 10]; units of relative signal strength magnitude such as the decibel 0.1[log 10] and bel [log 10], neper [log e], and other logarithmic-scale units such as the Richter magnitude scale point [log 10] or (more generally) the corresponding order-of-magnitude unit sometimes referred to as a factor of ten or decade (here meaning [log 10], not 10 years).
Motivation
The motivation behind the concept of logarithmic units is that defining a quantity on a logarithmic scale in terms of a logarithm to a specific base amounts to making a (totally arbitrary) choice of a unit of measurement for that quantity, one that corresponds to the specific (and equally arbitrary) logarithm base that was selected. Due to the identity
the logarithms of any given number a to two different bases (here b and c) differ only by the constant factor logc b. This constant factor can be considered to represent the conversion factor for converting a numerical representation of the pure (indefinite) logarithmic quantity Log(a) from one arbitrary unit of measurement (the [log c] unit) to another (the [log b] unit), since
For example, Boltzmann's standard definition of entropy S = k ln W (where W is the number of ways of arranging a system and k is Boltzmann's constant) can also written more simply as just S = Log(W), where "Log" here denotes the indefinite logarithm, and we let k = [log e]; that is, we identify the physical entropy unit k with the mathematical unit [log e]. This identity works because
Thus, we can interpret Boltzmann's constant as being simply the expression (in terms of more standard physical units) of the abstract logarithmic unit [log e] that is needed to convert the dimensionless pure-number quantity ln W (which uses an arbitrary choice of base, namely e) to the more fundamental pure logarithmic quantity Log(W), which implies no particular choice of base, and thus no particular choice of physical unit for measuring entropy.
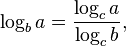
![\mathrm{Log}(a) = (\log_b a)[\log b] = (\log_c a)[\log c]. \,](../I/m/58ee2e3488b5ddad76ef2908936c273f.png)