Log structure

For log buildings, see log building.

In algebraic geometry, a log structure provides an abstract context to study semistable schemes, and in particular the notion of logarithmic differential form and the related Hodge-theoretic concepts. This idea has applications in the theory of moduli spaces, in deformation theory and Fontaine's p-adic Hodge theory, among others.

Motivation

The idea is to study some algebraic variety (or scheme) U which is smooth but not necessarily proper by embedding it into X, which is proper, and then looking at certain sheaves on X. The problem is that the subsheaf of $\mathcal{O}_X$ consisting of functions whose restriction to U is invertible is not a sheaf of rings (as adding two non-vanishing functions could provide one which vanishes), and we only get a sheaf of submonoids of $\mathcal{O}_X$ , multiplicatively. Remembering this additional structure on X corresponds to somehow remembering the inclusion 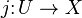$j \colon U \to X$ , which likens X with this extra structure to a variety with boundary (corresponding to 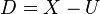$D = X - U$ ).^[1]

Definition

Let X be a scheme. A pre-log structure on X consists of a sheaf of (commutative) monoids 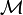$\mathcal{M}$ on X together with a homomorphism of monoids $\alpha \colon \mathcal{M} \to \mathcal{O}_X$ , where $\mathcal{O}_X$ is considered as a monoid under multiplication of functions.

A pre-log structure 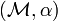$(\mathcal{M}, \alpha)$ is a log structure if in addition $\alpha$ induces an isomorphism 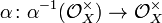$\alpha \colon \alpha^{-1}(\mathcal{O}_X^\times) \to \mathcal{O}_X^\times$ .

A morphism of (pre-)log structures consists in a homomorphism of sheaves of monoids commuting with the associated homomorphisms into $\mathcal{O}_X$ .

A log scheme is simply a scheme furnished with a log structure.

Examples

For any scheme X, one can define the trivial log structure on X by taking 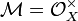$\mathcal{M} = \mathcal{O}_X^\times$ and $\alpha$ to be the identity.

The motivating example for the definition of log structure comes from semistable schemes. Let X be a scheme, 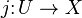$j \colon U \to X$ the inclusion of an open subscheme of X, with complement 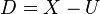$D = X - U$ a divisor with normal crossings. Then there is a log structure associated to this situation, which is $\mathcal{M} = \mathcal{O}_X \cap j_* \mathcal{O}_U^\times$ , with $\alpha$ simply the inclusion morphism into $\mathcal{O}_X$ . This is called the canonical (or standard) log structure on X associated to D.

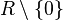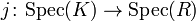Let R be a discrete valuation ring, with residue field k and fraction field K. Then the canonical log structure on $\mathrm{Spec}(R)$ consists of the inclusion of $R \setminus \{ 0 \}$ (and not $R^\times$ !) inside $R$ . This is in fact an instance of the previous construction, but taking $j \colon \mathrm{Spec}(K) \to \mathrm{Spec}(R)$ .

With R as above, one can also define the hollow log structure on $\mathrm{Spec}(R)$ by taking the same sheaf of monoids as previously, but instead sending the maximal ideal of R to 0.

Applications

One application of log structures is the ability to define logarithmic forms on any log scheme. From this, one can for instance define corresponding notions of log-smoothness and log-étaleness which parallel the usual definitions for schemes. This then allows the study of deformation theory.

In addition, log structures serve to define the mixed Hodge structure on any smooth variety X, by taking a compactification with boundary a normal crossings divisor D, and writing down the Hodge–De Rham complex associated to X with the standard log structure defined by D.^[2]

Log objects also naturally appear as the objects at the boundary of moduli spaces, i.e. from degenerations.

Log geometry also allows the definition of log-crystalline cohomology, an analogue of crystalline cohomology which has good behaviour for varieties that are not necessarily smooth, only log smooth. This then has application to the theory of Galois representations, and particularly semistable Galois representations.

References

↑ Arthur Ogus (2011). Lectures on Logarithmic Algebraic Geometry.
↑ Chris A.M. Peters; Joseph H.M. Steenbrink (2007). Mixed Hodge Structures. Springer. ISBN 978-3-540-77015-2

This article is issued from Wikipedia - version of the Thursday, November 20, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.