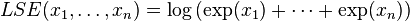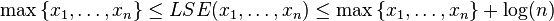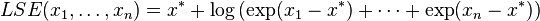LogSumExp
The LogSumExp (LSE) function is a smooth approximation to the maximum function, mainly used by machine learning algorithms. It's defined as the logarithm of the sum of the exponentials of the arguments:
The LogSumExp function domain is 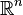 , the real coordinate space, and its range is
, the real coordinate space, and its range is 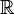 , the real line. The larger the values of
, the real line. The larger the values of 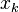 or their deviation, the better the approximation becomes. The LogSumExp function is convex, and is strictly monotonically increasing everywhere in its domain[1] (but not strictly convex everywhere [2]).
or their deviation, the better the approximation becomes. The LogSumExp function is convex, and is strictly monotonically increasing everywhere in its domain[1] (but not strictly convex everywhere [2]).
On the otherhand, when directly encountered, LSE can be well-approximated by 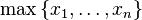 , owing to the following tight bounds.
, owing to the following tight bounds.
The lower bound is met when only one of the argument is non-zero, while the upper bound is met when all the arguments are equal.
log-sum-exp trick for log-domain calculations
The LSE function is often encountered when the usual arithmetic computations are performed in log-domain or log-scale.
Like multiplication operation in linear-scale becoming simple addition in log-scale; an addition operation in linear-scale becomes the LSE in the log-domain.
A common purpose of using log-domain computations is to increase accuracy and avoid underflow and overflow problems when very small or very large numbers are represented directly (i.e. in a linear domain) using a limited-precision, floating point numbers.
Unfortunately, the use of LSE directly in this case can again cause overflow/underflow problems. Therefore, the following equivalent must be used instead (especially when the accuracy of the above 'max' approx. is not sufficient). Therefore, many math libraries such as boost,IT++ etc. provide a default routine of LSE and use this formula internally.
where 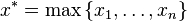
References
- ↑ El Ghaoui, Laurent (2015). Optimization Models and Applications.
- ↑ "convex analysis - About the strictly convexity of log-sum-exp function - Mathematics Stack Exchange". stackexchange.com.