Locally finite operator
In mathematics, a linear operator 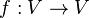 is called locally finite if the space
is called locally finite if the space  is the union of a family of finite-dimensional
is the union of a family of finite-dimensional  -invariant subspaces.
-invariant subspaces.
In other words, there exists a family 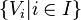 of linear subspaces of
of linear subspaces of  , such that we have the following:
, such that we have the following:
-
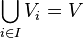
-
![(\forall i\in I) f[V_i]\subseteq V_i](../I/m/9e48771ee858230697dd9ff4b2701482.png)
- Each
 is finite-dimensional.
is finite-dimensional.
Examples
- Every linear operator on a finite-dimensional space is trivially locally finite.
- Every diagonalizable (i.e. there exists a basis of
 whose elements are all eigenvectors of
whose elements are all eigenvectors of  ) linear operator is locally finite, because it is the union of subspaces spanned by finitely many eigenvectors of
) linear operator is locally finite, because it is the union of subspaces spanned by finitely many eigenvectors of  .
.
This article is issued from Wikipedia - version of the Sunday, April 12, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.