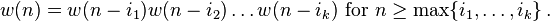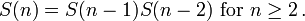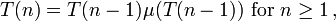Locally catenative sequence

In mathematics, a locally catenative sequence is a sequence of words in which each word can be constructed as the concatenation of previous words in the sequence.[1]

Formally, an infinite sequence of words w(n) is locally catenative if, for some positive integers k and i1,...ik:

w(n)=w(n-i_1)w(n-i_2)\ldots w(n-i_k) \text{ for } n \ge \max\{i_1, \ldots, i_k\} \, .

Some authors use a slightly different definition in which encodings of previous words are allowed in the concatenation.[2]

Examples

The sequence of Fibonacci words S(n) is locally catenative because

S(n)=S(n-1)S(n-2) \text{ for } n \ge 2 \, .

The sequence of Thue–Morse words T(n) is not locally catenative by the first definition. However, it is locally catenative by the second definition because

T(n)=T(n-1)\mu(T(n-1)) \text{ for } n \ge 1 \, ,

where the encoding μ replaces 0 with 1 and 1 with 0.

References

  1. ↑ Rozenberg, Grzegorz; Salomaa, Arto (1997). Handbook of Formal Languages. Springer. p. 262. ISBN 3-540-60420-0.
  2. ↑ Allouche, Jean-Paul; Shallit, Jeffrey (2003). Automatic Sequences. Cambridge. p. 237. ISBN 0-521-82332-3.
This article is issued from Wikipedia - version of the Saturday, May 23, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.