List of production functions

The production functions listed below, and their properties are shown for the case of two factors of production, capital (K), and labor (L), mostly for heuristic purposes. These functions and their properties are easily generalizable to include additional factors of production (like land, natural resources, entrepreneurship, etc.)

A production function can also be seen as the dynamics of national output/national income. This list is to collect production functions & the dynamics of national output/income that have been used in literature & textbooks.

Technology

There are three common ways to incorporate technology (or the efficiency with which factors of production are used) into a production function:

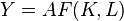
Hicks-neutral technology, or "factor augmenting": $\ Y = AF(K,L)$
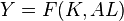
Harrod-neutral technology, or "labor augmenting": $\ Y = F(K,AL)$
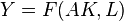
Solow-neutral technology, or "capital augmenting": $\ Y = F(AK,L)$

Elasticity of substitution

The elasticity of substitution between factors of production is a measure of how easily one factor can be substituted for another. With two factors of production, say, K and L, it is a measure of the curvature of a production isoquant. The mathematical definition is:

$\ \Epsilon=[\frac {\partial(slope)} {\partial(L/K)} \frac {L/K} {slope}]^{-1}$

where "slope" denotes the slope of the isoquant, given by:

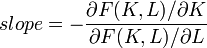
$\ slope=-\frac {\partial F(K,L)/ \partial K} {\partial F(K,L)/ \partial L}$

Returns to scale

Returns to scale can be

Increasing returns to scale: doubling all input usages more than doubles output.
Decreasing returns to scale: doubling all input usages less than doubles output.
Constant returns to scale: doubling all input usages exactly doubles output.

Some Famous forms

Constant elasticity of substitution (CES) function:

$Y = A[\alpha K^\gamma + (1-\alpha) L^\gamma]^{\frac{1}{\gamma}}$ , with $\gamma \isin [-\infty,1]$ which includes the special cases of:

Linear production (or perfect substitutes)

\ Y=A[\alpha K+ (1-\alpha) L]

when

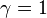
\ \gamma=1

Cobb-Douglas (or imperfect complements)

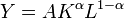\ Y=AK^\alpha L^{1-\alpha}

when

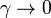
\gamma \to 0

Leontief production function (or perfect complements)

\ Y=Min[K,L]

when

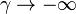
\gamma \to -\infty

Translog, a generealization of Cobb-Douglas, though not of CES

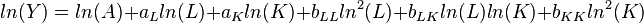
$\ ln(Y)=ln(A)+a_L ln(L)+a_K ln(K)+b_{LL} ln^2(L) + b_{LK} ln(L) ln(K) + b_{KK} ln^2(K)$

Factors

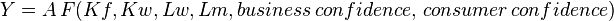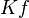Some authors also propose "indirect" production function. Production function can be assumed to have more factors in play, and with some factors refined. For instance, $Y=A\,F(Kf, Kw, Lw, Lm, business\, confidence, \, consumer \, confidence)$ while $Kf$ is the fixed capital, 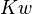$Kw$ is the working capital, 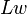$Lw$ is the working labor, 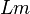$Lm$ is the management labor.

List of production functions

Technology

Elasticity of substitution

Returns to scale

Some Famous forms

Factors

See also